利用对极几何约束来检测动态特征点

方法介绍

对极几何约束常被用于检测特征点的运动状态，其原理示意图如Fig. 1所示：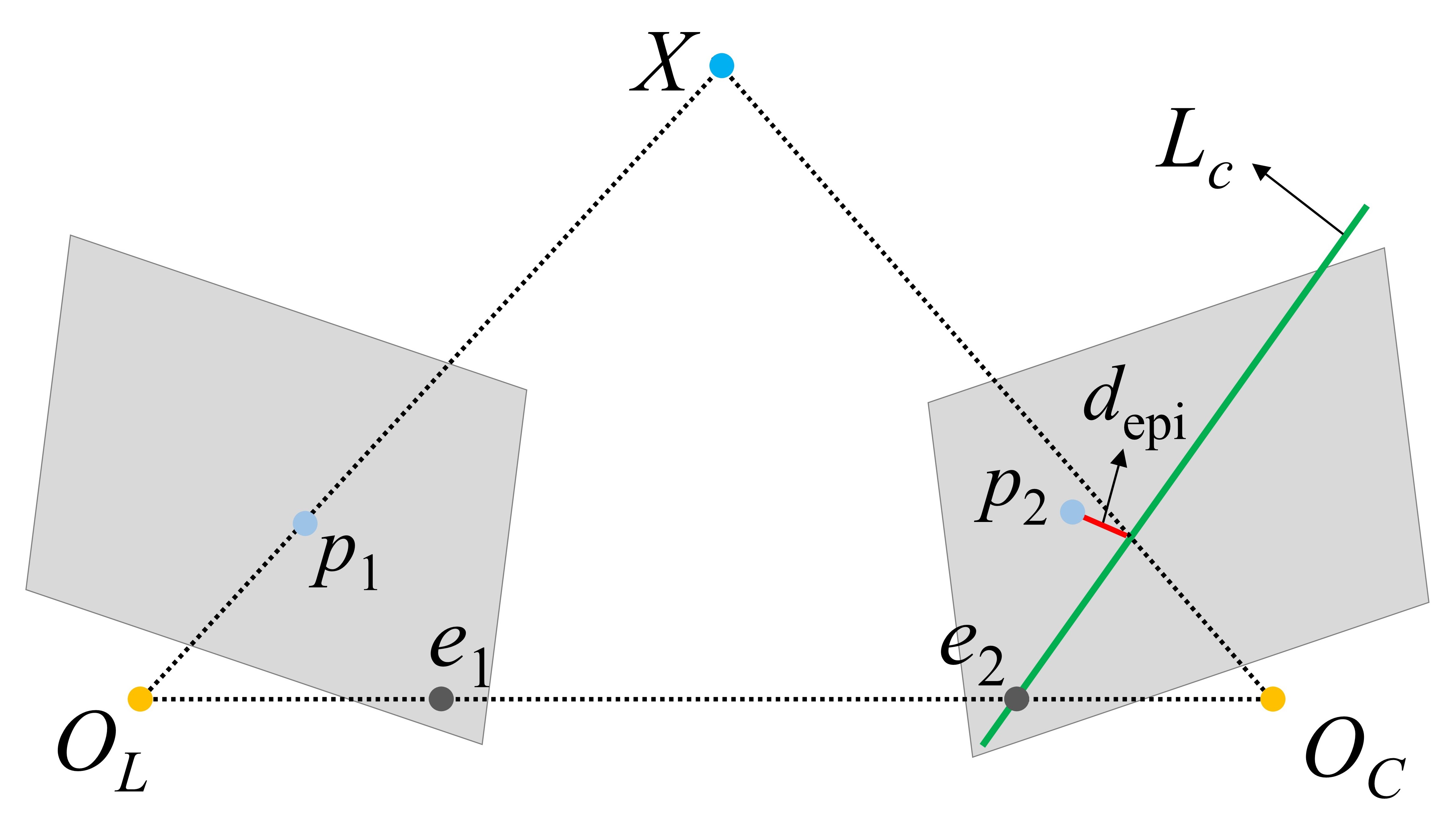


$X$ 是一地标点；$O_L$ ，$O_C$ 分别是两个相机的光心；$p_1$， $p_2$ 分别是 $X$ 在两个相机成像平面上的投影；$O_L$ ，$O_C$ 连线与成像平面的交点为极点 $e_1$， $e_2$ ；$O_L$ ，$O_C$，$X$ 形成的平面为极平面；极平面与成像平面的相交直线为极线 $L_c$。理想情况下，对于静态地标点 $X$ ，其投影点 $p_2$ 应该位于极线 $L_c$ 上，然而，现实中存在各种观测误差，导致 $p_2$ 与极线 $L_c$ 存在一定的距离 $d_{epi}$ ，对于静态地标点，该距离 $d_{epi}$ 应该较小，而动态地标点对应的距离 $d_{epi}$ 会很大，现有的动态特征检测方法多根据距离 $d_{epi}$ 与预设的阈值进行比较来判定该特征的运动状态。

然而，对极几何约束存在缺陷，当路标点 $X$ 在极平面上移动时，其投影点仍会位于极线或距离极线很近，那么，此时就无法使用对极几何约束来准确判断特征点的运动状态，这种情况称为degenerate motion，如Fig. 2所示。这种情况最常见于自动驾驶场景，动态车辆与自身的运动方向相同，此时难以利用对极几何约束实现对动态特征点的检测。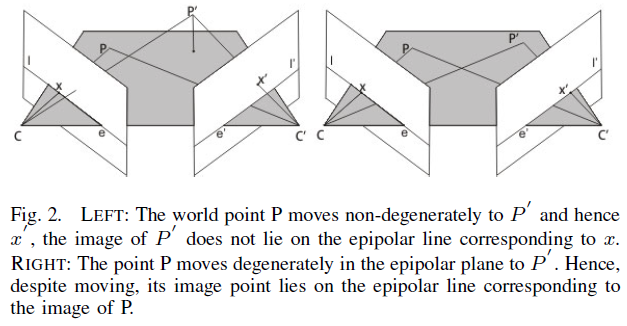

论文方法 & 问题

Kundu 等人[Kundu 等, 2009]提出了一种方法来应对此种情况，称为 Flow Vector Bound (FVB) ，现对该方法进行介绍，以及对其中发现的问题进行描述。

作者假设两个相机之间只存在一个平移 $\mathbf{t}=[t_1,t_2,t_3]^T$，以第一个相机的坐标系作为世界坐标系，则静态路标点 $X=[x,y,z]^T$ 与第一个成像平面上的投影 $p_1$ 分别为：

$$\displaylines{p_1 = \frac{1}{z}KX \\ X = zK^{-1}p_1 \tag{1}}$$

作者进而根据两个相机之间的平移转换，得到 $p_2$ 的坐标：

$$p_2 = K[I|\mathbf{t}]X = p_1+\frac{K\mathbf{t}}{z} \tag{2}$$

然后，作者根据上式得到同一特征点在两幅成像平面上的坐标差为 $K\mathbf{t}/z$ ，作者通过设定距离阈值来判断特征点的运动状态。

但是，我在推导中发现上式存在问题；而且，根据上式，由于图中的任一特征点具有相同的 $K\mathbf{t}$ ，那么所有的特征点应该具有相同的光流方向，无非是光流尺度不同罢了。然而，根据实际情况发现并不如此，如Fig. 3所示。可以发现，位于不同区域的特征点具有不同的光流方向，后文会继续推导该方向是由特征点在图片中的不同象限决定的。

推导过程

现在回到对 $p_2$ 的计算上去。$[I|\mathbf{t}]X$ 是将地标点 $X$ 从世界坐标系（相机1的坐标系）转换至相机2坐标系下，得到的坐标应为:

$$X_{C_2} = X + \mathbf{t} = [x+t_1, y+t_2, z+t_3]^T \tag{3}$$

然后，利用内参 $K$ 将其投影至成像坐标系中，在该过程中论文中的推导出现了问题，根据论文中的结果，反推其运算过程应为：

$$p_2 = \frac{1}{z}K[I|\mathbf{t}]X = \frac{1}{z}K(X+\mathbf{t}) = \frac{1}{z}K(zK^{-1}p_1+\mathbf{t}) = p_1+\frac{K\mathbf{t}}{z} \tag{4}$$

上述推导过程出错的地方在于，在相机2坐标系下，地标点 $X$ 的深度信息不再是 $z$ ，而应该是 $z+t_3$ 。则上式的正确推导过程为：

$$\displaylines{p_2 = \frac{1}{z+t_3}K[I|\mathbf{t}]X = \frac{1}{z+t_3}K(X+\mathbf{t}) \\ = \frac{1}{z+t_3}K(zK^{-1}p_1+\mathbf{t}) = \frac{1}{z+t_3}(zp_1 + K\mathbf{t}) \tag{5}}$$

那么，根据上式可以进一步得到特征点在两幅图片中的光流：

$$\displaylines{p_2-p_1 = [u_2,v_2]^T - [u_1,v_1]^T = [\Delta u, \Delta v]^T = \frac{1}{z+t_3}(K\mathbf{t} - t_3p_1) \\ K\mathbf{t} = [f_x t_1+c_x t_3, f_y t_2 + c_y t_3, t_3]^T = [M,N,t_3]^T \\ \Delta u = \frac{M - t_3 u_1}{z+t_3} \\ \Delta v = \frac{N - t_3 v_1}{z+t_3} \tag{6}}$$

上文也提到过，由于 $K\mathbf{t}$ 对于图中所有特征点是一致的，所以用 $M$, $N$ 分别表示前两个常数元素。值得注意的是，式（6）中的 $z+t_3$ 应该是一个正数，因为针孔相机模型只能映射位于相机前方的物体。

根据式（6）的结果可以看出，对于不同的特征点，其光流方向会根据其坐标位置而不同，即表现为 $\Delta u$, $\Delta v$ 会有正负。那么，进一步分析，不同位置特征点的光流方向具体表现为什么呢？根据Fig. 3 可以得到如Fig. 4 所示的区域光流方向分布情况，对于相机的纯移动情况，两幅成像平面中的极点相同，即 $e_1= e_2=$ Focus of Expansion (FOE)；且静态特征点的光流方向为沿着极点向外辐射移动。

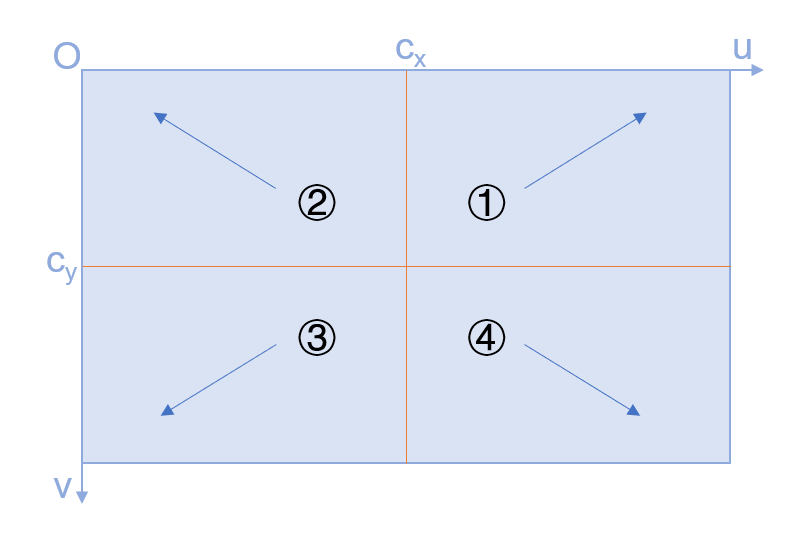
Fig. 4 是针对相机发生前向移动的情况，此时 $\mathbf{t} = [0,0,t_3]^T$ ，即相机只沿着z 轴进行前向移动；值得注意的是，$T_{C_2W} = [I|\mathbf{t}]$ 是从世界坐标系（相机1坐标系）转换为相机2坐标系，此处的 $t_3 < 0$ 。由此，可对 $\Delta u, \Delta v$ 进一步更新：

$$\displaylines{\Delta u = \frac{M - t_3 u_1}{z+t_3} = \frac{t_3 (c_x - u_1)}{z+t_3} \\ \Delta v = \frac{N - t_3 v_1}{z+t_3} = \frac{t_3 (c_y - v_1)}{z+t_3} \tag{7}}$$

以象限①内的特征点为例，该象限内特征点 $u_1 > c_x, v_1 < c_y$ ，则 $\Delta u > 0, \Delta v < 0$ ，与实际光流方向契合。由此证明了式（6）的正确。

参考文献

[1] Kundu, Abhijit, K. Madhava Krishna, and Jayanthi Sivaswamy. “Moving object detection by multi-view geometric techniques from a single camera mounted robot.” 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2009.