1 介绍

最近使用两个Flir相机采了数据，打算在ORB-SLAM2系列代码上进行测试，采集完数据后需要对双目相机进行标定，在网上搜寻了相关资料后，发现使用Matlab工具库可以比较方便地进行双目相机的标定，在此记录一下。注：双目标定部分主要参考了该文章。

简单记录一下相机的相关参数：

名称	参数
型号	FLIR BFS-U3-31S4
分辨率	2048*1536
最大帧率	55 FPS
快门类型	全局快门
传感器型号	Sony IMX265, CMOS

2 标定图片采集

2.1 标定棋盘

标定棋盘可以从网上下载，也可使用程序生成特定参数的图片，此处可参考OpenCV网站提供的成品图片或生成程序。将生成的图片保存下来，并进行打印，在打印时选择1:1比例即可。

注：本人尝试了使用上文所述的OpenCV提供的成品图片与生成程序制作的图片，在打印后使用直尺测量棋盘网格大小，发现均无法实现严格定义的尺寸，不知道是不是打印时出现了问题；后面在进行标定时，手动量了网格大小作为标定参数。

2.2 图片采集

为了保证标定效果，建议将标定棋盘放在不同的位置，抓拍十张以上的照片。该文章介绍了棋盘图的拍摄规范，现记录如下：

在一次标定的整个过程中，不能调节相机的光圈、焦距。也就是说，在标定过程中，要保证摄像头进光量与焦距的一致，每次改变参数均需重新进行标定。
把相机图像分成四个象限，应保证拍摄的标定板图像均匀分布在五个位置（四个象限以及正中心）中，且在每个位置进行不同方向的两次倾斜，参考fig 2；或者，也可以固定住标定板，移动相机在不同角度进行拍摄。

图片参考自文章。
标定板的成像应大致占摄像头视野的1/4左右。
标定板成像不能过曝，过曝会导致特征轮廓的提取的偏移。
拍摄过程中可以对标定板适当的进行补光，调节标定板到镜头的距离，以便于拍出清晰的图片。
标定图片数量通常在15~25张之间，数量太少，标定的参数会不准确。
标定时用的标定板最好选择x方向与y方向棋盘格不同的，便于标定程序识别标定板方向。

按照以上采集规则采集标定图片即可。

3 标定过程

使用Matlab标定的过程如下所示：

打开Matlab，在命令行窗口输入stereoCameraCalibrator：

然后会跳出fig 4所示的窗口，点击Add Images：

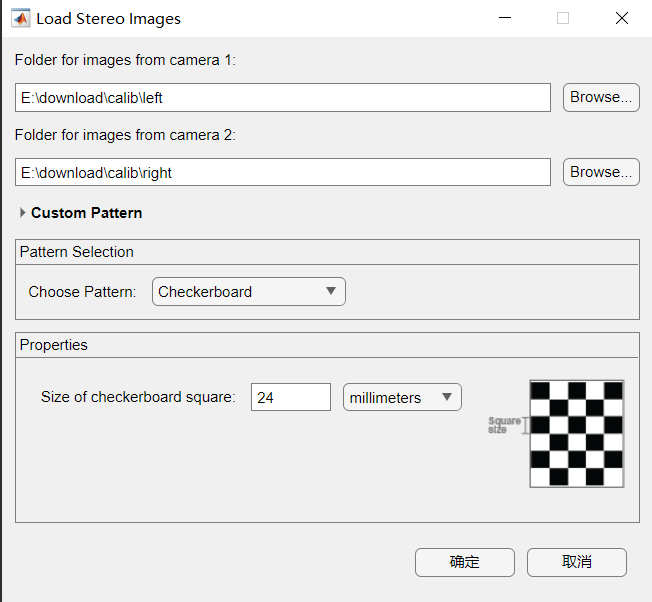
在弹出的窗口中分别输入左图、右图的文件夹路径，并设置网格的尺寸（注意，此处的网格尺寸本人是使用实际测量得到的尺寸），：

然后点击确定，Matlab开始对标定图片进行处理：

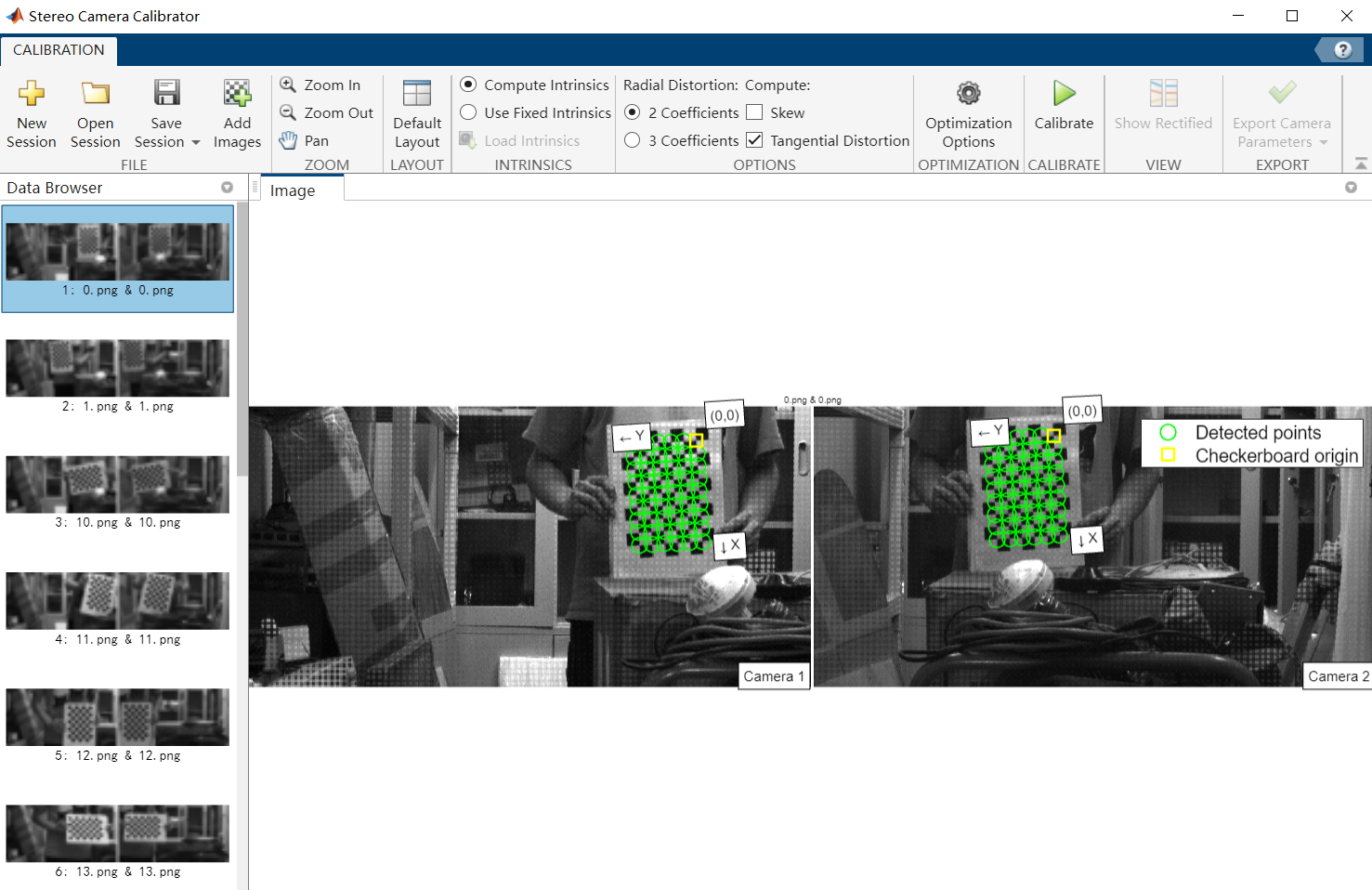
接下来对标定参数进行设定：

选择 Compute Intrinsics；
选择 2 Coefficients（注：3 Coefficients是针对鱼眼相机标定的）；
选择 Tangential Distortion（注：无需勾选Skew，否则相机内参标定结果中会出现参数s，即相机内参矩阵的第一行会变成[fx, s, u0]，与OpenCV的参数格式不同）；
点击Calibrate按钮进行标定计算。

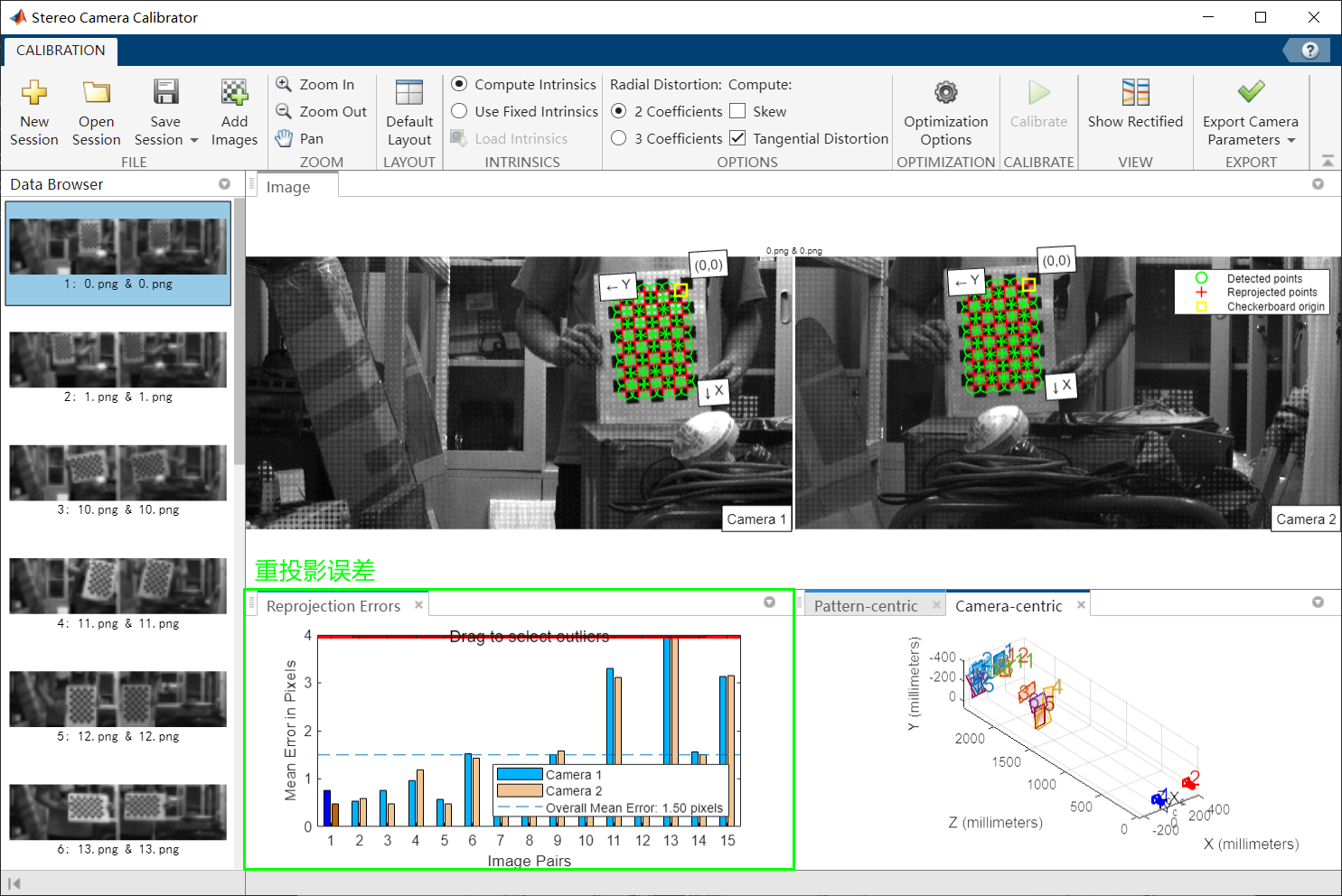
然后即可得到标定后的结果，fig 8左下区域表示重投影误差，对误差较大的图片进行剔除，来实现达到较低像素精度的表现（Overall Mean Error小于0.1 pixels）。

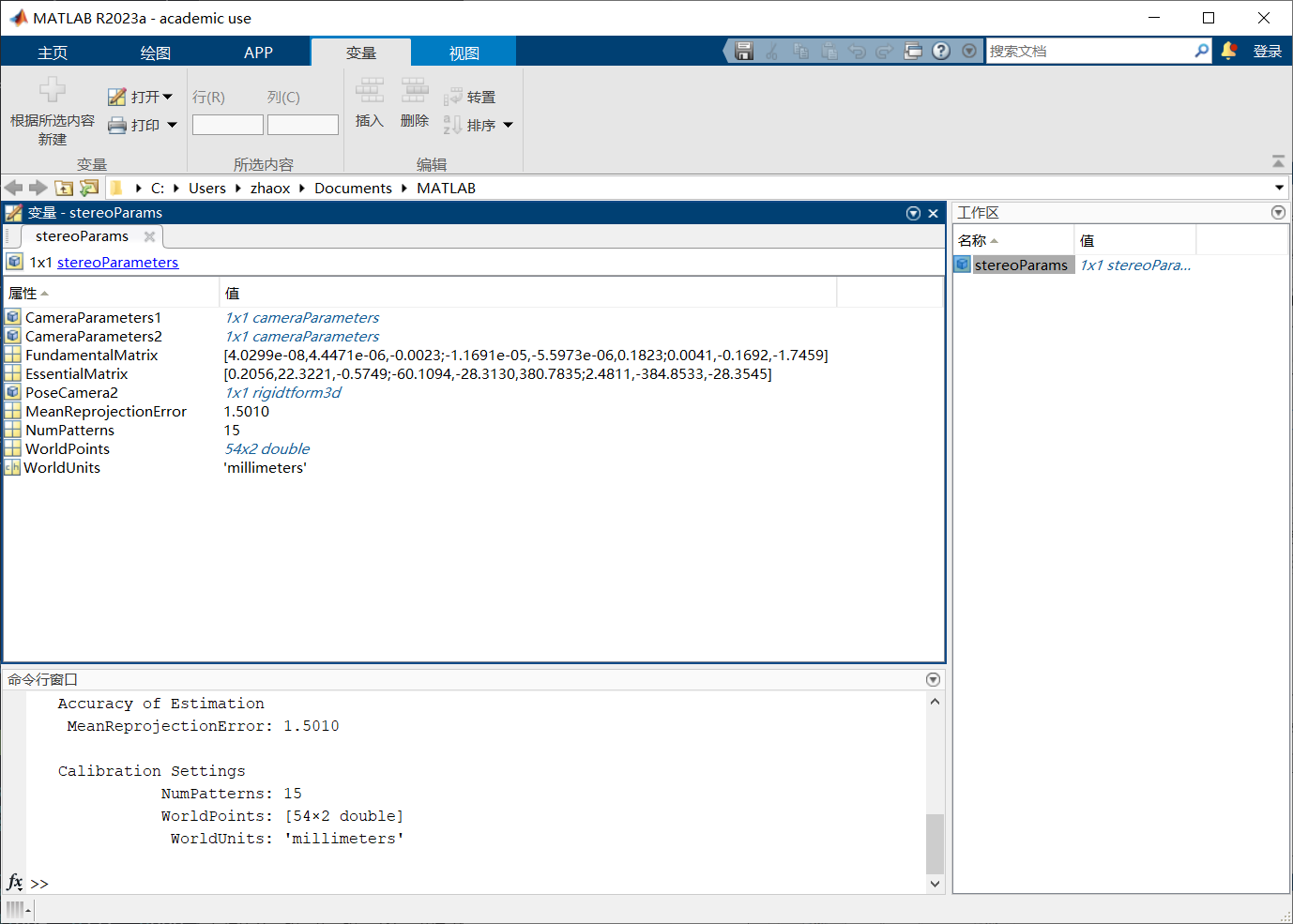
最后，点击Export Camera Parameters按钮，即可返回工作区查看标定结果：

stereoParams.CameraParameters1
- K：左相机内参矩阵；
- RadialDistortion：左相机径向畸变参数 k1, k2, k3，只有两个数值时表示 k3 = 0；
- TangentialDistortion：左相机切向畸变参数 p1, p2。
stereoParams.CameraParameters2 参数同上
stereoParams.PoseCamera2
- R: 左相机到右相机的旋转矩阵；本次标定得到的参数为
  
  0.995139840336347 -0.00663565457289115 0.0982479835097892
  -0.000660670904084147 0.997254587919016 0.0740462719414676
  -0.0984695977919431 -0.0737513048214236 0.992403387412513
  
  可以看到，由于两个相机固定位置较好，旋转矩阵基本为一个单位矩阵；
- Translation: 左相机到右相机的平移向量；本次标定得到的参数为
  
  [-3.858979029808597e+02,-2.237062834310436,-22.218127814587270]

记录一下OpenCV的相机参数格式：

内参矩阵:
$\begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}$

畸变向量: $(k_1, k_2, p_1, p_2, k_3)$

4 双目相机校正

4.1 校正原理介绍

经过上述双目标定过程，可以获取双目相机的内参：$f_x, f_y, c_x, c_y$ ，畸变系数：$k_1, k_2, k_3, p_1, p_2$ ，以及两个相机之间的旋转矩阵和平移向量：$\mathbf{R}, \mathbf{T}$。双目相机的校正过程主要包括去畸变与立体校正两个步骤：

去畸变：主要是对两个相机的径向畸变、切向畸变进行处理；
立体校正：双目相机主要作用是利用视差对双目匹配点进行测距，该过程是在双目系统处于理想共面行对准情况下进行的：即两个相机成像平面位于同一平面上，两成像平面之间只有平移变换。这样即可保证真实世界的3D点在双目系统中的投影像素位于同一水平线上，只需对双目图片进行单行搜索即可完成双目特征点匹配。立体校正过程如Fig 10所示。

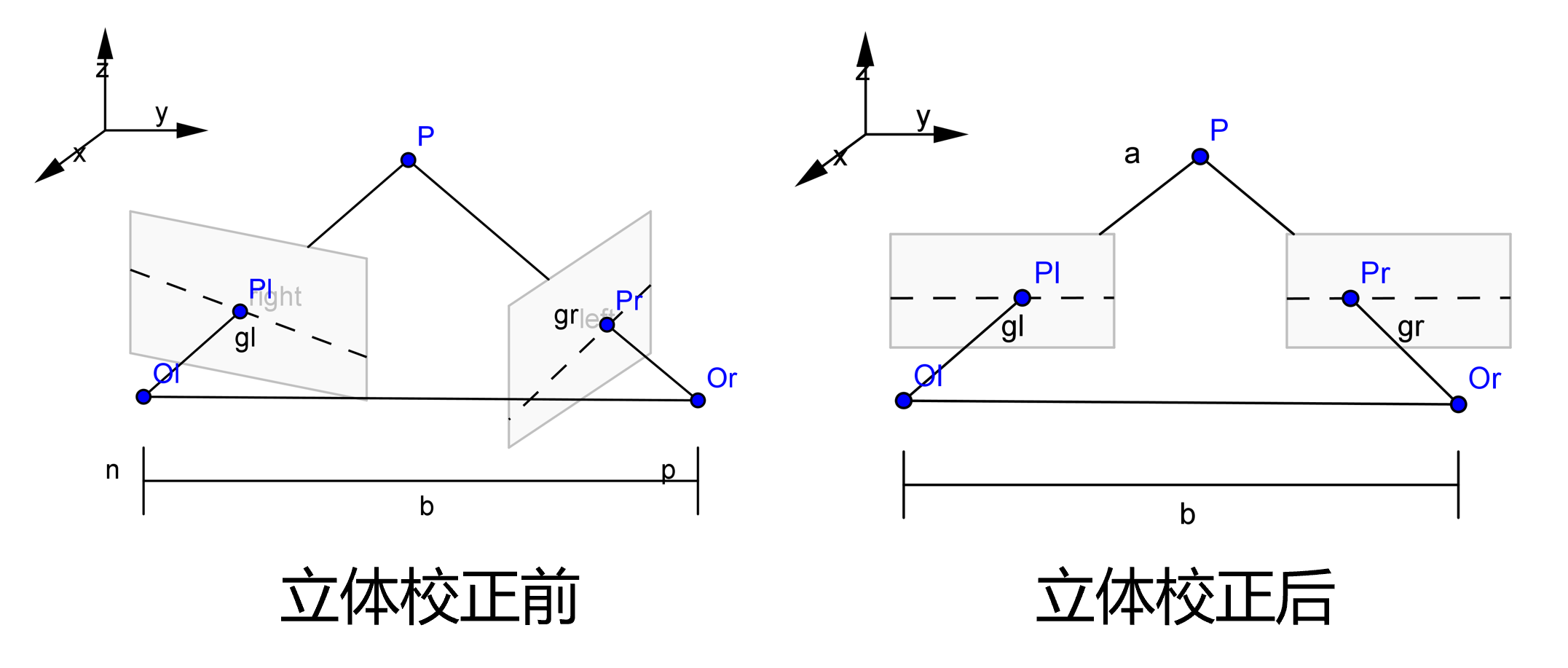
经过立体校正之后，即可根据双目匹配点进行深度获取，该过程如Fig 11所示：

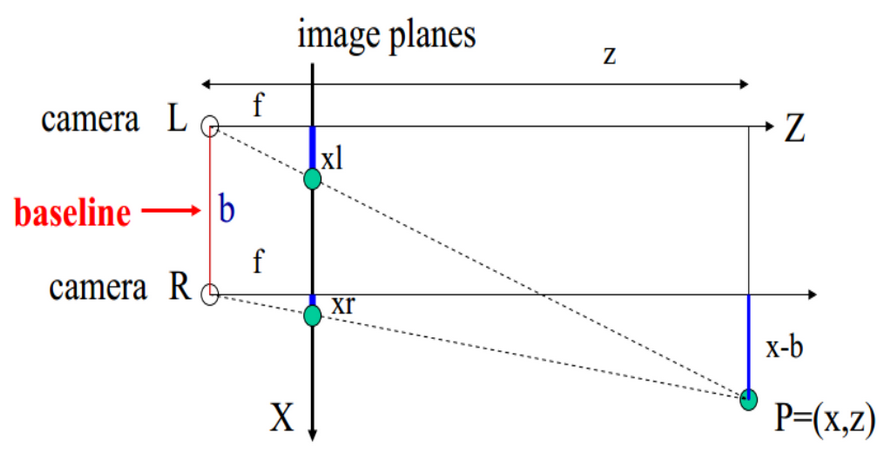
根据比例关系，可以求得深度信息：$z = \frac{bf}{x_l - x_r} = \frac{bf}{d}$ ，其中，$d$ 即为视差。此处参考文章。

4.2 OpenCV双目校正过程

在OpenCV中，立体校正的流程如下所示：

利用 stereoRectify() 函数实现Bouguet算法，得到立体校正所需的变换矩阵和投影矩阵；
将上步得到的变换矩阵和投影矩阵传入 initUndistortRectifyMap() 函数，生成校正图像到原始图像的映射关系；
根据映射关系，利用 remap() 函数将原图像处理为校正后的双目图像。

校正过程的代码如下所示：

R1, R2, P1, P2, Q, roi1, roi2 = cv2.stereoRectify(kLeft, coeffsLeft, kRight, 
                                                  coeffsRight, (width, height), 
                                                  R, T, alpha=-1)
    
map1x, map1y = cv2.initUndistortRectifyMap(kLeft, coeffsLeft, R1, P1,
                                               (width, height), cv2.CV_16SC2)
map2x, map2y = cv2.initUndistortRectifyMap(kRight, coeffsRight, R2, P2,
                                               (width, height), cv2.CV_16SC2)

rectifiedLeftImg = cv2.remap(leftImg, map1x, map1y, cv2.INTER_LINEAR)
rectifiedRightImg = cv2.remap(rightImg, map2x, map2y, cv2.INTER_LINEAR)

4.3 校正前后图片对比

利用上述过程对双目系统进行校正，校正前后的对比如下所示：

Echo's blog

双目相机的标定与校正