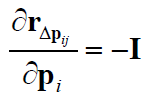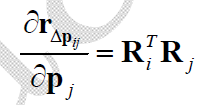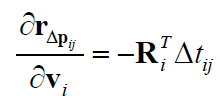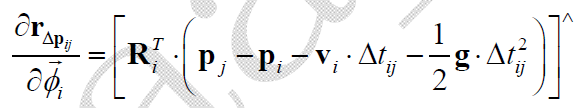注:本文是对北航邱笑晨博士总结的预积分公式推导过程进行记录,由于是个人简单记录,所以基本上内容、公式都是截取自该文章。
1 IMU 测量模型(Sensor Model)和运动学模型(Kinetic Model)
陀螺测量模型:
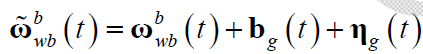
其中,$\mathbf{b}_g$ 是bias,$\mathbf{\eta}_g$ 是白噪声。该模型利用了static world assumption:考虑到MEMS IMU 的观测精度,以及SLAM 的运动场景较小,因此忽略地球自转(认为地球是static world),并假设运行区域水平面是个平面,重力矢量 $\mathbf{g}^w$ 的指向固定且模值恒定。
加速度计测量模型:
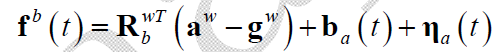
其中,$\mathbf{b}_a$ 是bias,$\mathbf{\eta}_a$ 是白噪声。
运动模型的微分方程:
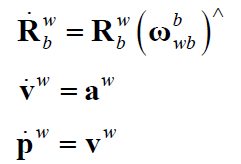
注:观察旋转的微分形式,斜对称矩阵在右边,说明这是在body 参考系下的,参照文章。
运动方程的离散形式:
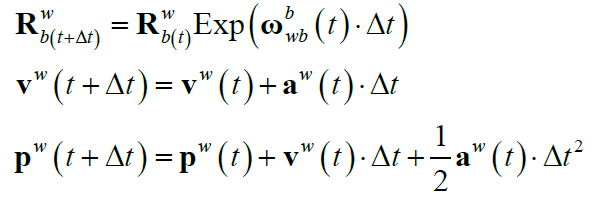
将测量模型代入离散运动方程有:

离散噪声和连续噪声的协方差有如下关系:
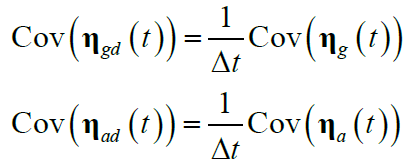
进一步假设 $\Delta t$ 恒定(即采样频率固定),使用 $k = 0, 1, 2, …$ 表示采样的离散时刻,则离散运动方程可进一步简化为:
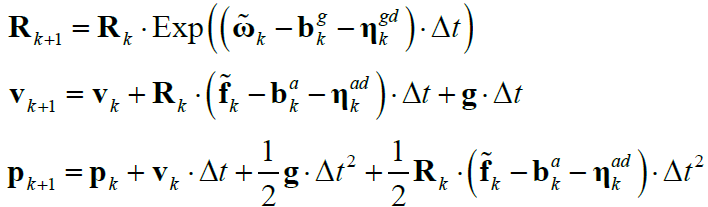
2 IMU 预积分
当IMU 参与的组合导航时,IMU 的采样频率一般高于其他传感器,所以会将一段时间内的IMU 观测数据进行积分作为整个观测,以参与同其他传感器的组合求解,如利用 $k=i$ 时刻与 $k=j-1$ 时刻内所有的IMU 观测,基于 $k=i$ 时刻的 $\mathbf{R}_i, \mathbf{v}_i, \mathbf{q}_i$ 直接更新 $k=j$ 时刻的 $\mathbf{R}_j, \mathbf{v}_j, \mathbf{q}_j$ :
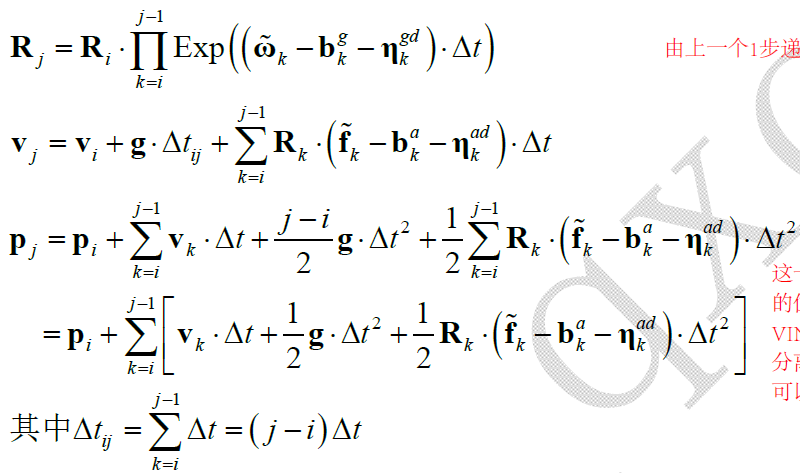
在每次优化迭代后,会得到新的 $\mathbf{R}_i, \mathbf{v}_i, \mathbf{q}_i$ ,则上式中的积分操作就需要重新计算一遍,导致运算量极大。而IMU 预积分的思路就是把每次优化迭代时不变的项提取出来,以减小每次重新积分的计算量;即剥离出与更新量无关的参数(在上式中,更新量为 $\mathbf{R}_i, \mathbf{v}_i, \mathbf{q}_i$ 和 bias),得到 $k=i,k=j$ 之间的相对变化量,这样在每次迭代更新后只需要重新计算与更新量相关的项即可。根据上式获取的预积分项为:
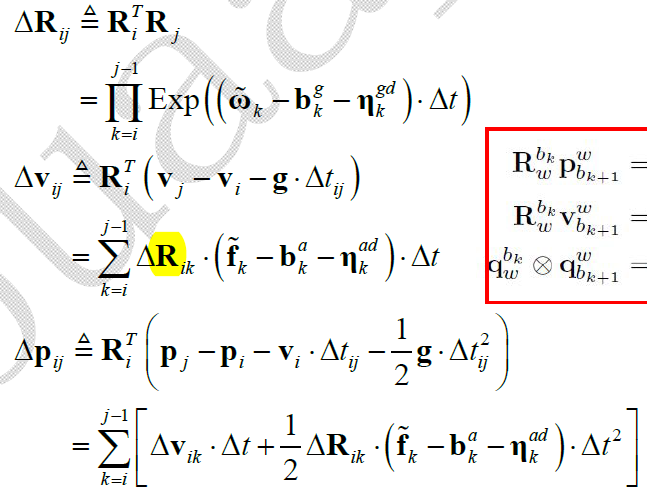
此处可进一步参考文章的讲解,如下图所示,绿色部分即为与更新量相关的项,蓝色部分表示与更新量无关的项,$\alpha$ 相当于上式中的 $\Delta \mathbf{p}_{ij}$ ,$\beta$ 相当于上式中的 $\Delta \mathbf{v}_{ij}$ 。
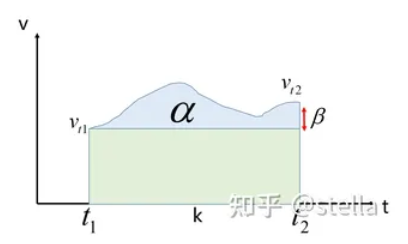
3 预积分测量值与测量噪声
将噪声项 ($\eta^{gd}_k, \eta^{ad}_k$) 从预积分项中分离出来,获得 “预积分测量值 = 理想值 + 白噪声” 的形式。首先做一个假设:在与积分时间内bias保持不变,即 $\mathbf{b}_{i}^g = \mathbf{b}_{i+1}^g = … = \mathbf{b}_{j}^g, \mathbf{b}_{i}^a = \mathbf{b}_{i+1}^a = … = \mathbf{b}_{j}^a$ 。
3.1 测量值
3.1.1 旋转预积分项
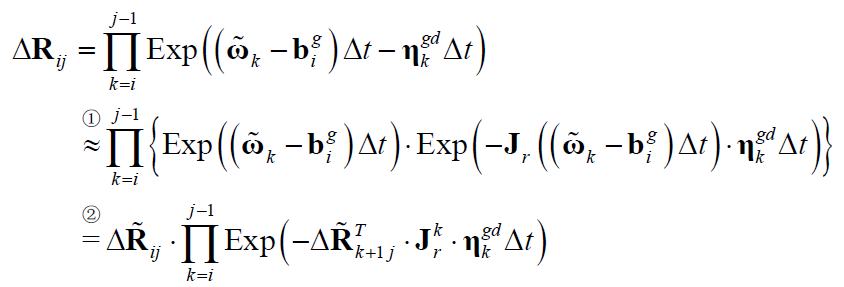
其中,① 处使用了旋转矩阵的右乘小量扰动;② 处使用了Adjoint 性质,对 “ABABAB…AB” 连乘进行转换顺序即可。
对于上式,令
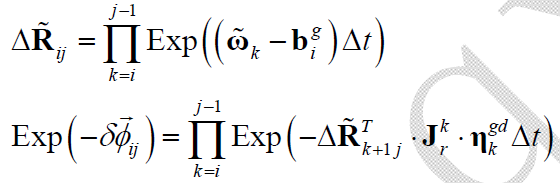
则有:
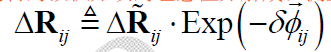
从而获得了旋转预积分项 “预积分测量值 = 理想值 + 白噪声” 的形式,其中,$\Delta \tilde{\mathbf{R}}_{ij}$ 为预积分测量值,由陀螺仪测量值和对陀螺仪bias 的估计值计算得到;$\delta \overrightarrow{\phi}_{ij}$ 为测量噪声。
补充说明:
Adjoint 性质表示如下:
$Exp(\phi)\cdot \mathbf{R} = \mathbf{R} \cdot Exp(\mathbf{R}^T \phi)$
证明过程如下所示:
首先,令 $Exp(\phi) = exp(\hat{\phi}) = exp(\theta \hat{\mathbf{a}})$ ,然后
其中,用到了 $\mathbf{R}\hat{\mathbf{a}}\mathbf{R}^T = \hat{(\mathbf{R}\mathbf{a})}$ 的性质,该性质的证明可参考文章。
3.1.2 速度预积分项
将上节获取的旋转预积分项代入 $\Delta \mathbf{v}_{ij}$ 中,可得:
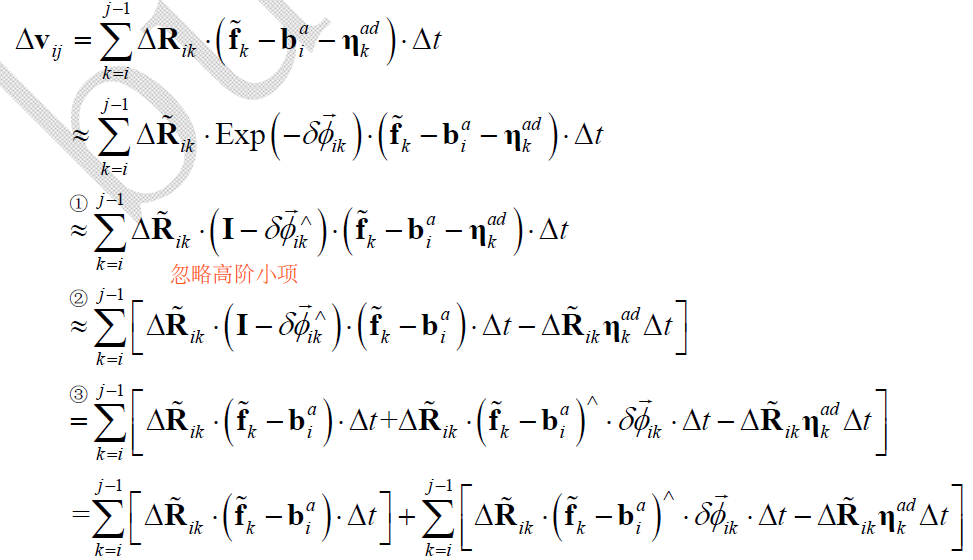
对于上式,令:
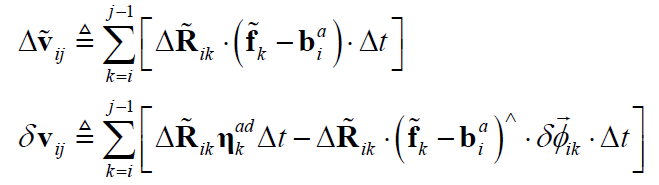
则有:
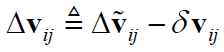
从而获得了速度预积分项 “预积分测量值 = 理想值 + 白噪声” 的形式,其中,$\Delta \tilde{\mathbf{v}}_{ij}$ 为预积分测量值,由IMU 测量值和对bias 的估计值计算得到;$\delta \mathbf{v}_{ij}$ 为测量噪声。
3.1.3 位置预积分项
将旋转预积分项、速度预积分项代入 $\Delta \mathbf{p}_{ij}$ 中,有:

对于上式,令:
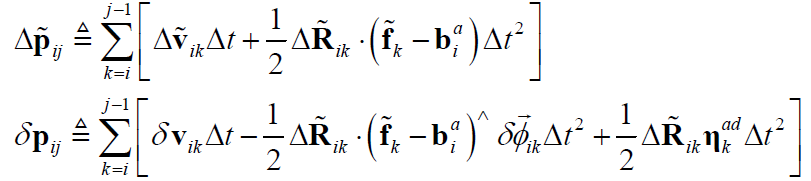
则有:
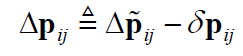
从而获得了位置预积分项 “预积分测量值 = 理想值 + 白噪声” 的形式,其中,$\Delta \tilde{\mathbf{p}}_{ij}$ 为预积分测量值,由IMU 测量值和对bias 的估计值计算得到;$\delta \mathbf{p}_{ij}$ 为测量噪声。
3.1.4 总结
对前三节获取的预积分项理想值与测量值之间的关系汇总如下:
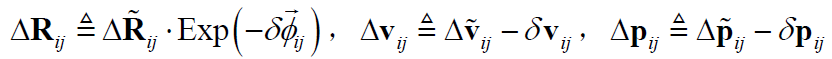
代入预积分项理想值的表达式:
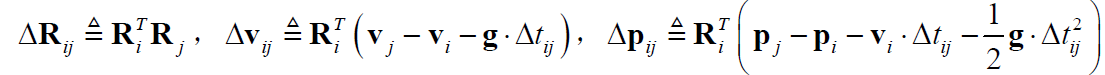
则有:
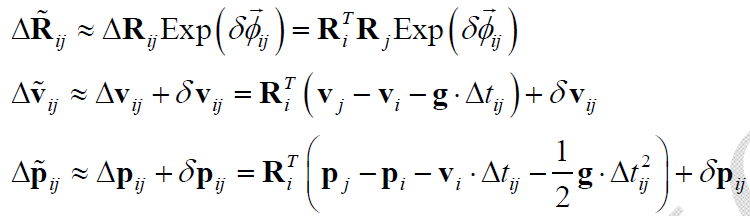
上式即为最终的 “测量值=真实值 + 测量噪声” 的模式。
3.2 测量噪声分析
将预积分测量噪声表示为:
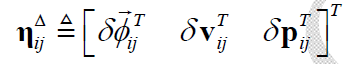
希望其满足高斯分布,则对 $\eta_{ij}^\Delta$ 进行分析。
3.2.1 旋转预积分测量噪声
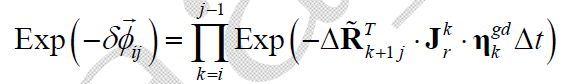
其中,$\mathbf{J}_r^k = \mathbf{J}_r((\tilde{\omega}_k - \mathbf{b}_i^g)\Delta t)$ 。对上式两侧取对数:
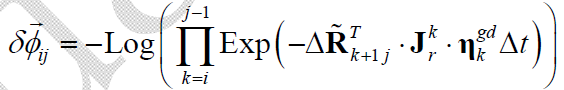
对上式进行处理:
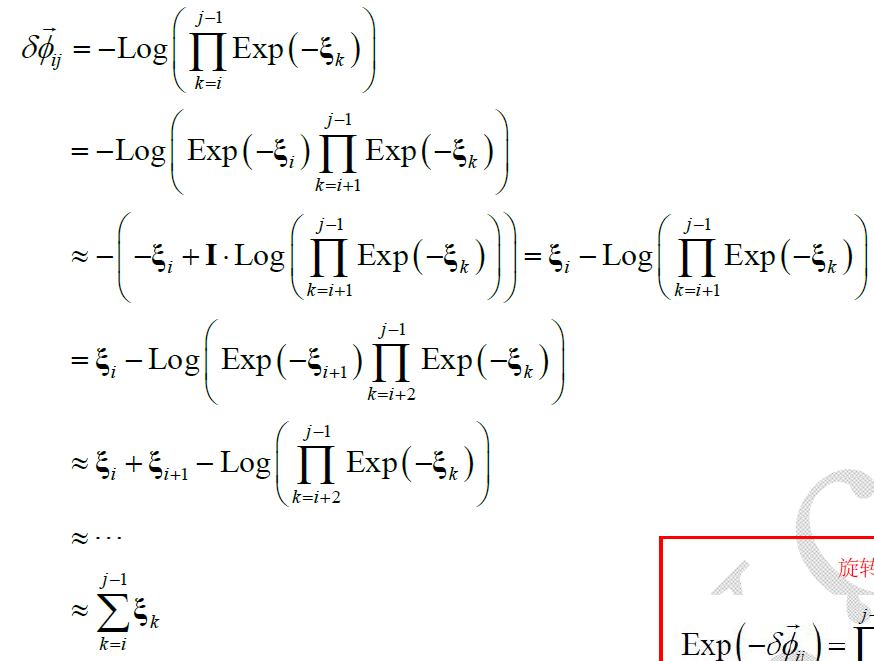
即:
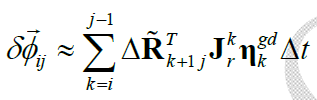
由于 $\Delta \tilde{\mathbf{R}}_{k+1,j}^T, \mathbf{J}_r^k, \Delta t$ 均是已知量,而 $\eta_k^{gd}$ 是零均值高斯噪声,因此,$\delta \overrightarrow{\phi}_{ij}$ 也是零均值高斯噪声。
在此基础上,进一步推导旋转预积分测量噪声的递推形式,对于 $\delta \overrightarrow{\phi}_{ij-1}\rightarrow \delta \overrightarrow{\phi}_{ij}$ ,有:
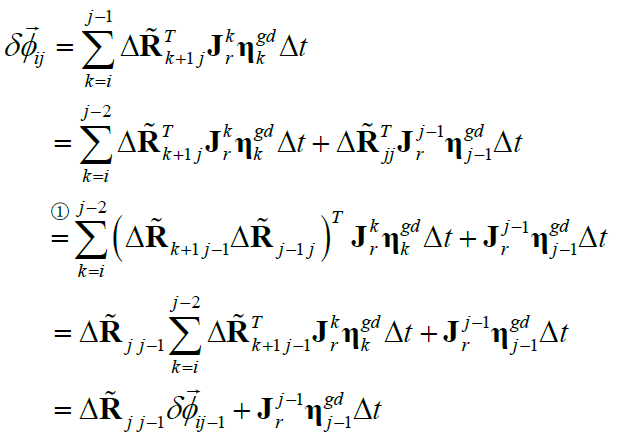
3.2.2 速度预积分测量噪声
由于$\delta \overrightarrow{\phi}_{ij}$ 近似为零均值高斯噪声,且 $\eta_k^{ad}$ 也是零均值高斯噪声,则根据 $\delta \mathbf{v}_{ij}$ 表达式可知其也具有高斯分布的性质:
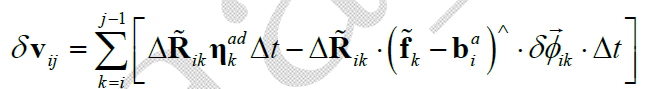
在此基础上,进一步推导速度预积分测量噪声的递推形式,对于 $\delta \mathbf{v}_{ij-1}\rightarrow \delta \mathbf{v}_{ij}$ ,有:
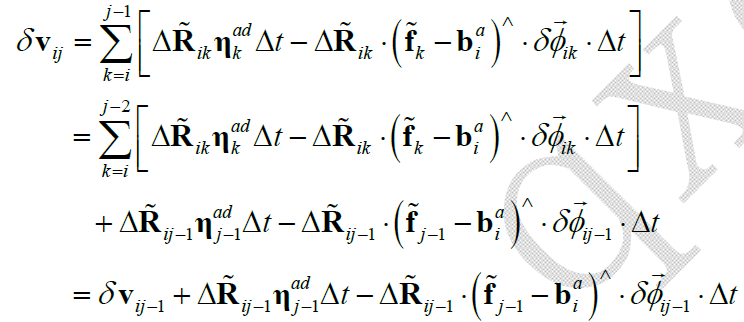
3.2.3 位置预积分测量噪声
类似 $\delta \mathbf{v}_{ij}$ , $\delta \mathbf{p}_{ij}$ 也具有高斯分布的性质:
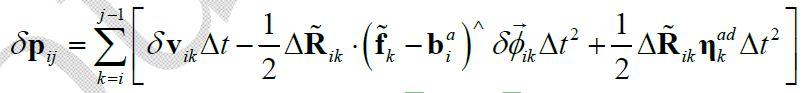
在此基础上,进一步推导速度预积分测量噪声的递推形式,对于 $\delta \mathbf{p}_{ij-1}\rightarrow \delta \mathbf{p}_{ij}$ ,有:
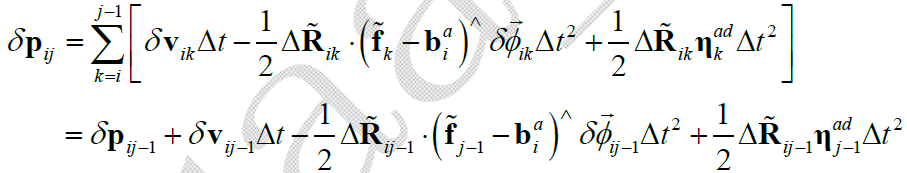
3.2.4 总结
综上所述,可以得到预积分测量噪声 $\eta_{ij}^\Delta$ 的递推形式:

其中,$\eta_k^d = [(\eta_k^{gd})^T, (\eta_k^{ad})^T]^T$ 。若令:
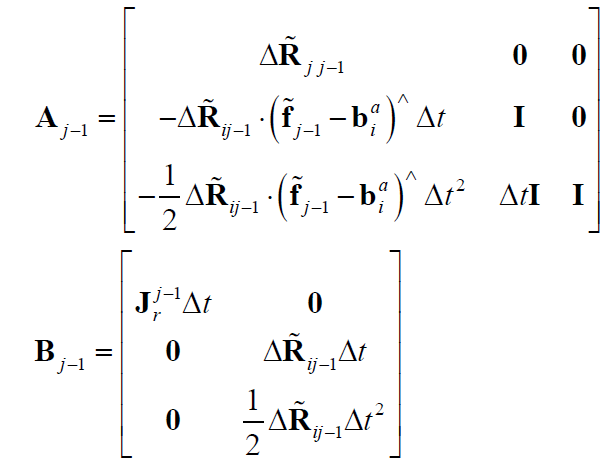
则有:
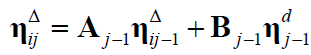
相应地,预积分测量噪声的协方差矩阵的递推计算形式为:
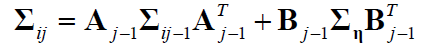
3.3 bias 更新时的预积分测量值更新
前面的预积分计算是在积分区间bias 固定的假设下进行的,当bias 变化时为了减小预积分测量值计算的负担,利用线性化进行预积分项的一阶近似更新。对bias 更新过程进行如下定义:
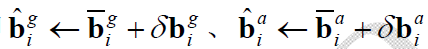
其中,$\overline{\mathbf{b}}$ 表示旧的bias,$\delta{\mathbf{b}}$ 表示bias变化量,$\hat{\mathbf{b}}$ 表示更新后的bias。预积分项的线性化更新过程如下所示:
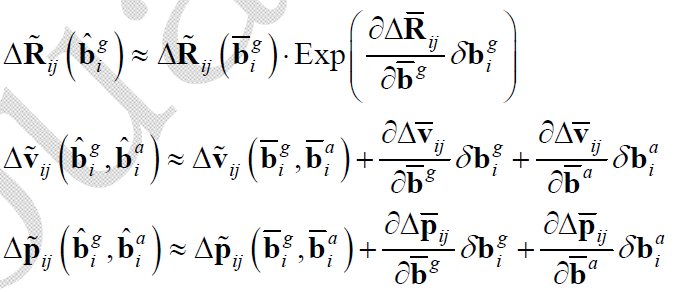
上式简写为:
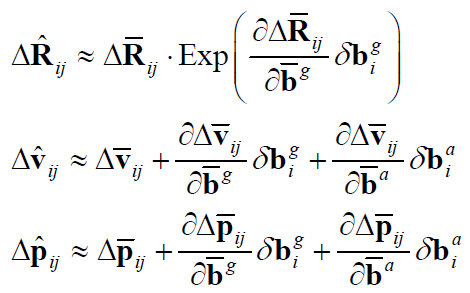
3.3.1 旋转预积分bias更新偏导项求解
求解过程如下所示:

对上式进行同样的利用Adjoint性质对连乘顺序进行调整,即可得到:
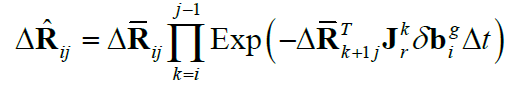
当 $\mathbf{c}_k$ 极小时,有 $\mathbf{J}_r(\mathbf{c}_k) \approx \mathbf{I}$ ,对上式进一步处理可得到:
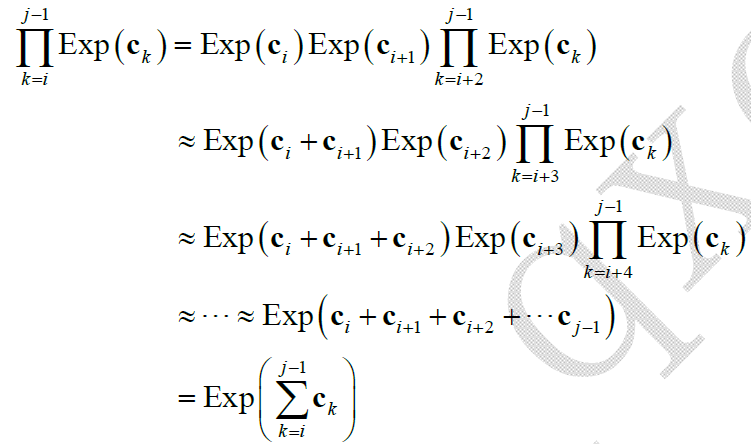
由此可以得到:
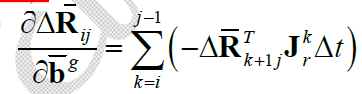
其中,$\mathbf{J}_r^k = \mathbf{J}_r((\tilde{\omega}_k - \overline{\mathbf{b}}_i^g)\Delta t)$。
3.3.2 速度预积分bias更新偏导项求解
与旋转预积分类似,可以得到两个偏导项为:
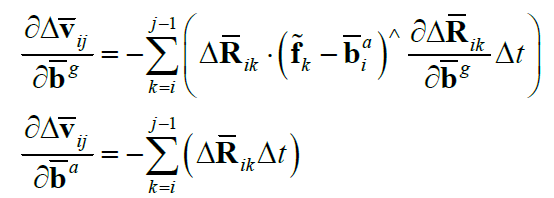
3.3.3 位置预积分bias更新偏导项求解
位置预积分的两个偏导项为:
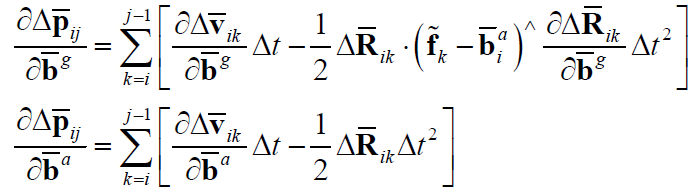
4 残差及Jacobian
4.1 残差项
预积分项的理想值为:
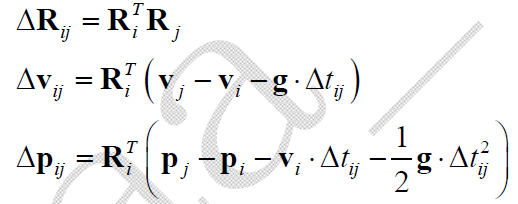
当状态参数更新时,形成的残差为:
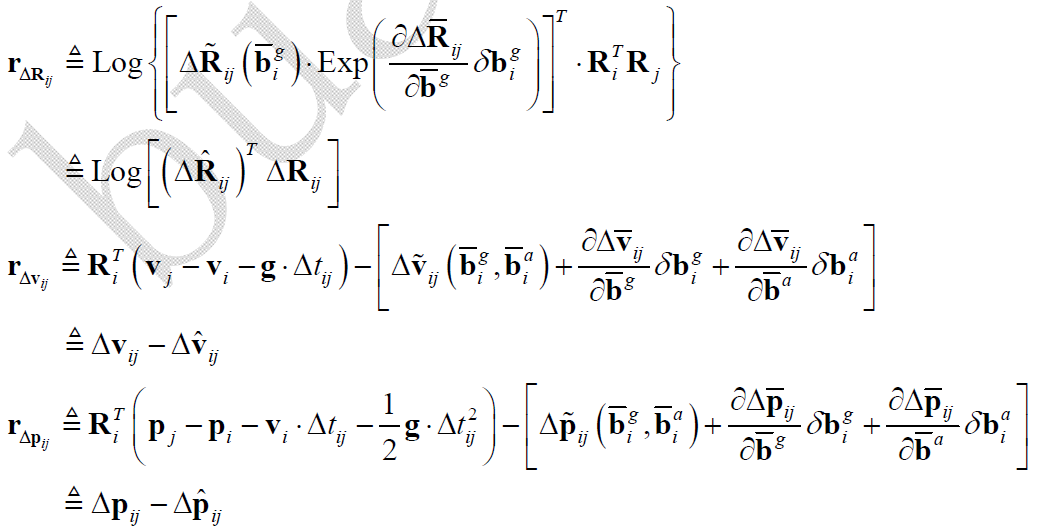
即,残差定义为 “残差 = 理想值 - 后验观测值”。
状态参数的更新过程表示为:
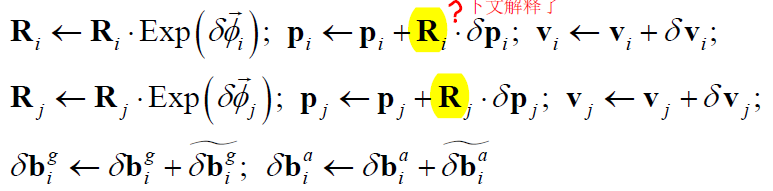
在迭代优化中,待优化的状态参数为 $\mathbf{R}_i, \mathbf{p}_i, \mathbf{v}_i, \mathbf{R}_j, \mathbf{p}_j, \mathbf{v}_j, \delta \mathbf{b}_i^g, \delta \mathbf{b}_i^a$ ,而迭代中求解增量方程得到的增量是:$\delta \overrightarrow{\phi}_i,\delta\mathbf{p}_i, \delta\mathbf{v}_i, \delta \overrightarrow{\phi}_j,\delta\mathbf{p}_j, \delta\mathbf{v}_j, \tilde{\delta \mathbf{b}_i^g}, \tilde{\delta \mathbf{b}_i^a}$ ,最后两项是bias增量的增量。
4.2 Jacobian
求残差项($\mathbf{r}_{\Delta \mathbf{R}_{ij}}, \mathbf{r}_{\Delta \mathbf{v}_{ij}}, \mathbf{r}_{\Delta \mathbf{p}_{ij}}$ )关于各个状态参数的Jacobian。
4.2.1 旋转残差项Jacobian
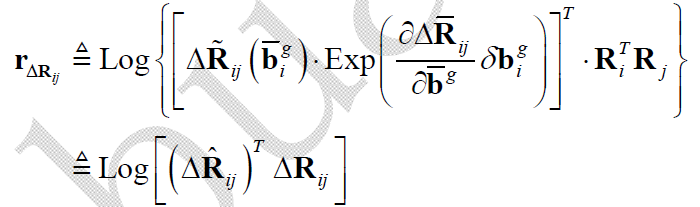
首先是“0类”:
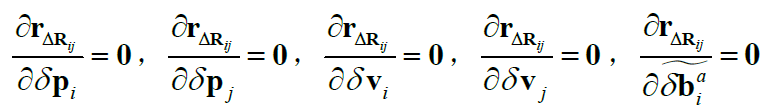
注:上式中应该是写错了,应是对状态参数进行Jacobian求解,而不是对状态参数的增量进行求解。
然后是“复杂类”:
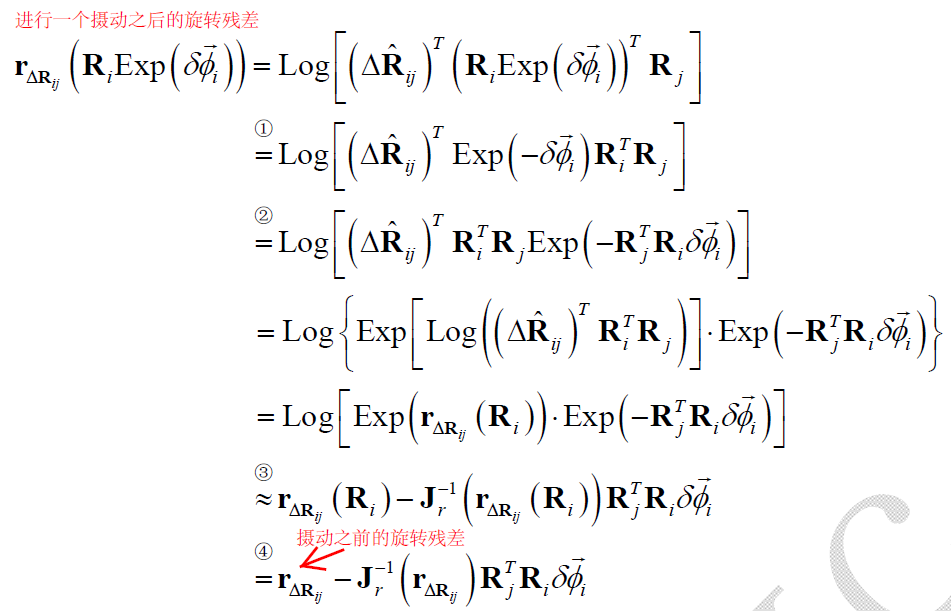
由此得到 $\mathbf{r}_{\Delta \mathbf{R}_{ij}}$ 关于 $\overrightarrow{\phi}_i$ 的Jacobian:
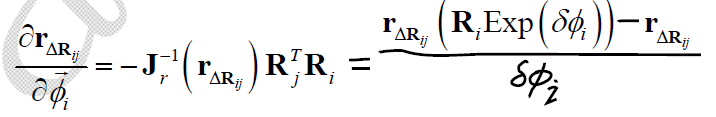
同样地,可得到 $\mathbf{r}_{\Delta \mathbf{R}_{ij}}$ 关于 $\overrightarrow{\phi}_j, {\delta \mathbf{b}_i^g}$ 的Jacobian:
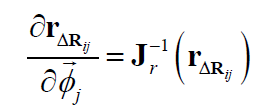
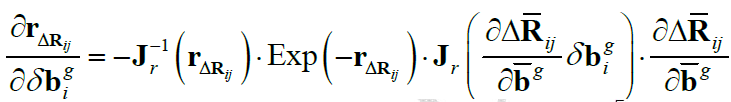
4.2.2 速度残差项Jacobian
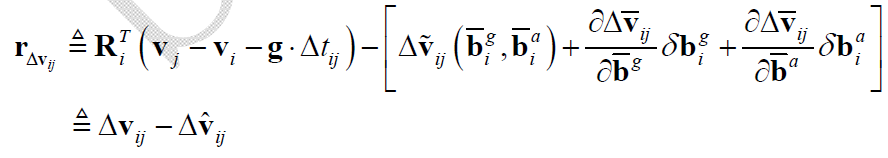
首先是“0类”:
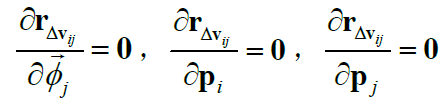
然后是“线性类”:
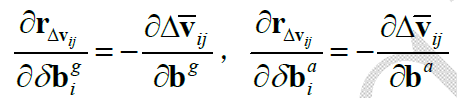
最后是“复杂类”,$\mathbf{r}_{\Delta \mathbf{v}_{ij}}$ 关于 $\mathbf{v}_i, \mathbf{v}_j, \overrightarrow{\phi}_i$ 的Jacobian:
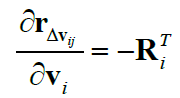
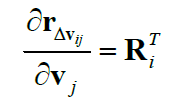
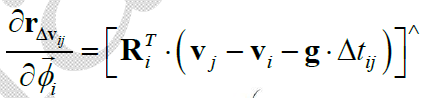
4.2.3 位置残差项Jacobian
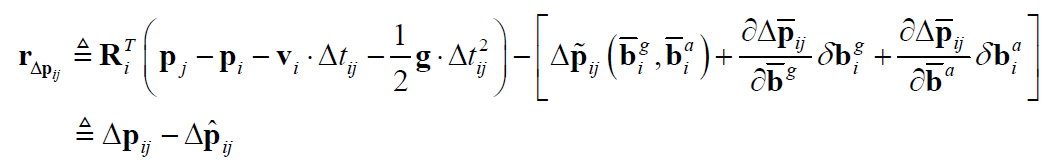
首先是“0类”:
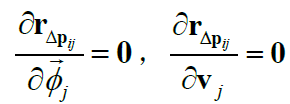
然后是“线性类”:
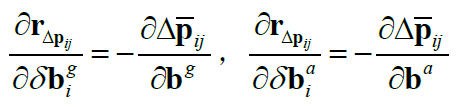
最后是“复杂类”,$\mathbf{r}_{\Delta \mathbf{p}_{ij}}$ 关于 $\mathbf{p}_i, \mathbf{p}_j, \mathbf{v}_i, \overrightarrow{\phi}_i$ 的Jacobian: