Echo's blog
0%

论文记录 ORB-SLAM3_An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM

发表于 更新于 分类于 ， ，

Campos, Carlos, Richard Elvira, Juan J. Gómez Rodríguez, José M. M. Montiel, and Juan D. Tardós. “ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM.” IEEE Transactions on Robotics 37, no. 6 (December 2021): 1874–90. https://doi.org/10.1109/TRO.2021.3075644.

1 Introduction

ORB-SLAM3 的主要创新点包括：

  1. 一个单目、双目视觉-惯性SLAM 系统。该系统完全依赖MAP 最大后验估计，即使是在IMU 初始化阶段。
  2. 增强型地点识别技术。现有的许多SLAM、VO 系统使用DBoW2 进行地点识别，但DBoW2 在检查几何一致性之前需要进行时间一致性检测，即匹配连续三个关键帧，这增加了地点识别的代价，导致回环检测或者地图重用的速度很慢。针对于此，作者提出了一个新颖的地点识别算法：对候选关键帧首先进行几何一致性检测，然后与三个共视关键帧进行局部一致性检测 *local consistency*。
  3. ORB-SLAM Atlas。第一个可以处理单目和双目视觉&视觉-惯性系统的完整多地图SLAM 系统。该地图集可表示一组不连续的地图，并顺滑地使用所有的地图操作，包括：地点识别、相机重定位、回环检测以及精确地图融合等。
  4. 抽象的相机参数化表示使得SLAM 系统可以兼容不同映射模型的相机，如针孔相机、鱼眼相机等。

3 System Overview

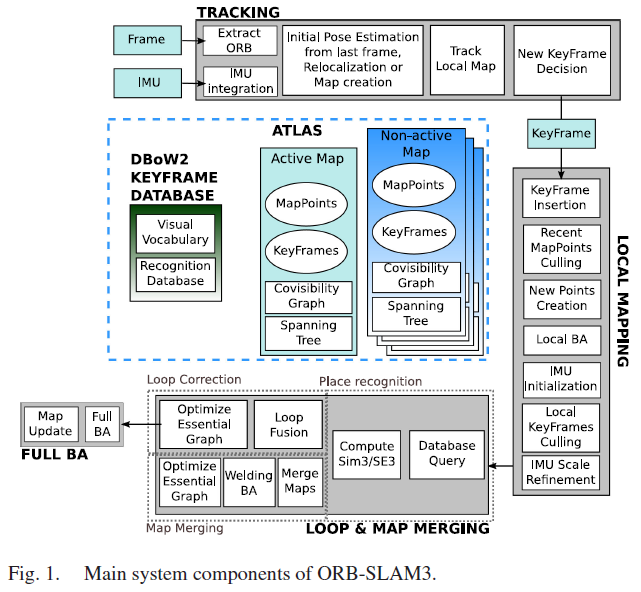
ORB-SLAM3 整体架构如Fig.1所示，较ORB-SLAM2 有以下特性：

  1. Atlas包含一组不连续的地图，包含活动地图和非活动地图；该系统建立了一个独特的关键帧DBoW2 数据库用于重定位、回环检测和地图融合。
  2. 跟踪线程与实时地图相结合，利用最小化重投影误差来计算相机的位姿；在VI （visual-inertial）模式下，通过将惯导残差包含进优化过程实现对载体速度、IMU 偏差的计算。当跟踪失败时，跟踪线程会在地图集中所有的地图上进行重定位。
  3. 局部制图线程在VI 模式下会对IMU 参数进行初始化及优化。
  4. 回环与地图融合线程以关键帧的速率检测活动地图与整个地图集之间的共同区域，以进行回环检测和地图融合。

fig1

4 Camera Model

作者的目标是通过提取所有与相机模型相关的属性和函数（投影方程、Jacobian 等）来实现对相机模型的抽象化，这使得该系统可以兼容任意类型的相机。

经典的SLAM 算法默认使用针孔相机模型，会对整幅图片或特征坐标进行矫正，使得该系统运行在一个理想的平面视网膜上。然而，该方法不适用于具有超大FOV 的鱼眼相机，鱼眼相机获取的图片中，边缘处的物体会被放大，中间部分的物体不清晰，无法使用图片矫正进行处理；而对特征坐标进行矫正需要FOV 小于180°，而且与经典SLAM 算法的特征重投影误差在整个平面上服从均匀分布的假设不符。而对鱼眼图片进行裁剪又会失去其大视角的优势。

4.1 Relocalization

ORB-SLAM 是通过ePnP 算法来解决重定位问题的，这个算法是基于校准过的针孔相机模型，因此，需要对该算法进行修改以适应不同的相机模型，这里，作者使采用了最大似然PnP 算法来解决该问题。

4.2 Nonrectified Stereo SLAM

双目相机默认使用针孔相机投影模型进行矫正，并认为两幅图片对齐至水平极线，从而对两幅图中的特征在同一行中进行匹配，但这些假设过于严格，且不适用于鱼眼相机。因此，作者在本系统中不依赖于图片矫正，而是将双目相机是做两个独立的单目相机，并满足以下特性：

  1. 固定的位姿转换关系 SE(3)；
  2. 两幅图中有公共的观测区域。

5 Visual-Inertial SLAM

5.1 Fundamentals

在VI 中，代求的参数较纯视觉SLAM 更多，除了位姿 $\mathbf{T}_i = [\mathbf{R}_i, \mathbf{p}_i]$ 外，还包括速度 $\mathbf{v}_i$ ，陀螺仪和加速度计偏差 $\mathbf{b}_i^g, \mathbf{b}_i^a$ ，即状态向量为：

f1

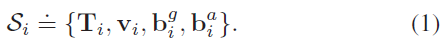
对于VI SLAM，对连续帧之间的IMU 观测进行预积分，获取预积分得到的旋转、速度和位置观测，表示为 $\Delta \mathbf{R}_{i, i+1}， \Delta \mathbf{v}_{i, i+1}，\Delta \mathbf{p}_{i, i+1}$ ，以及相应的协方差矩阵 $\sum_{\mathcal{I}_{i, i+1}}$ 。给定这些预计分项和状态 $\mathcal{S}_i, \mathcal{S}_{i+1}$ ，定义如下所示的惯导残差 $\mathbf{r}_{\mathcal{I}_{i, i+1}}$ ：

f2

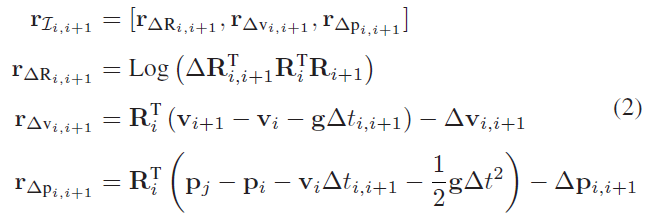
其中， $Log: SO(3) -> \mathbb{R}^3$ 将李群映射至向量空间。

相机观测特征点的重投影误差项：

f3

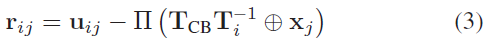
其中，$\Pi: \mathbb{R}^3 -> \mathbb{R}^n$ 表示不同相机模型对应的投影方程；$\mathbf{T}_{CB} \in SE(3)$ 表示从body-IMU 到相机的位姿转换矩阵（根据标定已知）；$\mathbf{x}_j$ 表示3D 物体地标。

结合惯导和视觉的观测残差，VI SLAM 的优化问题可表示为：

f4

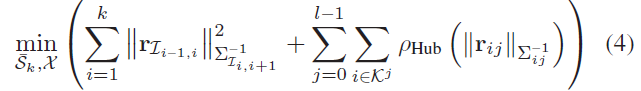
其中，$\overline{\mathcal{S}}_k, \chi$ 分别表示 k+1 个关键帧状态向量和 l 个3D 观测地标点；$\mathcal{K}^j$ 表示观测到3D 地标点 j 的关键帧集合。

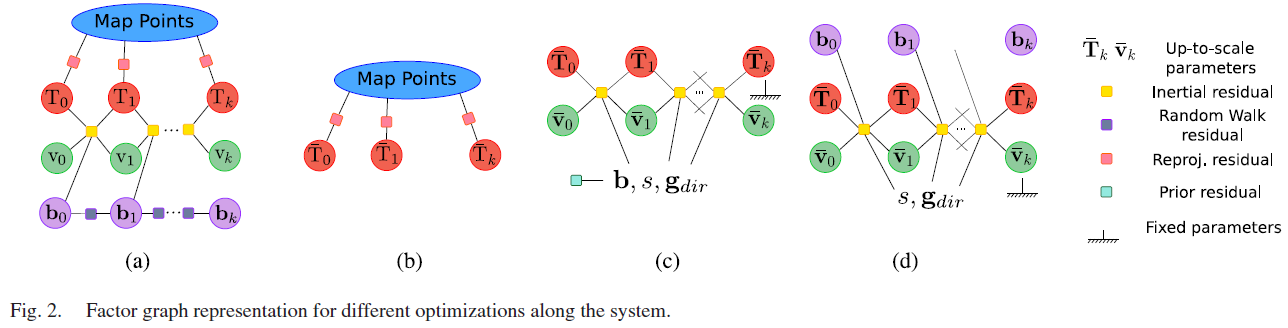
该优化问题可通过Fig.2（a）所示的因子图进行表示，该优化需要进行效率上的优化，更关键的是，需要一个良好的初始化来收敛到精确解。

fig2

5.2 IMU Initialization

这一步的目标在于获取较好的IMU 参数初始值：速度、重力方向以及IMU 偏差。作者基于以下几点见解提出了一种快速且准确的初始化方法：

  1. 单目SLAM 可以提供非常精确的初始化地图，但主要问题在于尺度未知；解决这个问题可以增强IMU 初始化能力。
  2. 有研究表明，相较于将尺度视为BA 的一个隐含表示，直接将其视为一个待优化参数可以极大加速其收敛过程。
  3. 在IMU 初始化中忽略传感器不确定度会造成较大的误差。

为了较好地考虑传感器的不确定度，作者将IMU 初始化看作一个MAP 估计问题，分为以下三步进行：

  1. 纯视觉的MAP 估计：以纯视觉单目SLAM 运行2s，关键帧速率为4Hz，进行仅包含视觉的BA 优化（Fig.2（b）），得到相机位姿和特征点，以及相应的比例尺地图；将位姿转换至载体坐标系，得到相应的轨迹 $\overline{\mathbf{T}}_{0:k} = [\mathbf{R}, \overline{\mathbf{p}}]_{0:k}$ ，其中，上划线表示单目情况下的尺度不确定性。

  2. 纯惯导的MAP 估计：该步骤目的在于仅利用 $\overline{\mathbf{T}}_{0:k}$ 和惯导观测的情况下，获取惯导参数的MAP 估计，状态向量表示为：

    f5

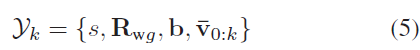
    其中，s 表示尺度参数；$\mathbf{R}_{wg} \in SO(3)$ 表示计算重力向量 $\mathbf{g}$ 在世界坐标系下的旋转矩阵，表示为 $\mathbf{g} = \mathbf{R}_{wg} \mathbf{g}_I$ ，其中，$\mathbf{g}_I = (0,0,G)^T$ ；$\mathbf{b} = (\mathbf{b}^a, \mathbf{b}^g) \in \mathbb{R}^6$ 表示加速度计和陀螺仪的偏差，在初始化过程中假定为固定常数；$\overline{\mathbf{v}}_{0:k}$ 表示尺度不定的载体速度，利用 $\overline{\mathbf{T}}_{0:k}$ 进行初始估计。此阶段只考虑惯导观测，则后验分布表示为：

    f6

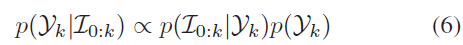
    考虑到观测之间的独立性，上式可进一步转换为：

    f7

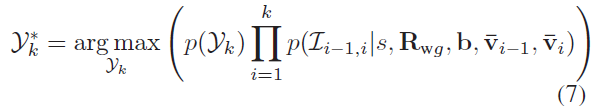
    转换为-log 形式，并假设IMU 预积分误差服从高斯分布，则最终优化问题表示为：

    f8

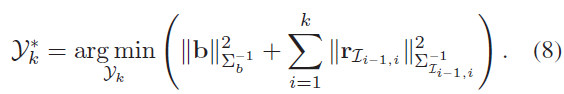
    该优化过程如Fig.2（c）所示，其中，矩阵 $\sum_b^{-1}$ 表示IMU 偏差取值范围的先验知识。

    由于重力方向的旋转不会改变重力，则 $\mathbf{R}_{wg}$ 的更新过程为：

    f9

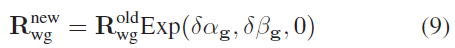
    为了保证尺度因子保持为正数，定义其更新为：

    f10

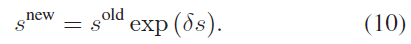
  3. VI MAP 估计：在前获取了视觉和惯导的良好初始化估计的基础上，可以进行VI 联合优化来对参数进行细调优化，该过程可表示为 Fig.2（a）。

作者提出的这个初始化方法较现有的方法具有较大的优势，且在公开数据集EuRoC 上进行了测试，可在2s 初始化后实现5%的尺度误差，为了进一步提高初始化估计精度，在初始化后5s、15s进行VI BA，可实现1%尺度误差的效果。同时，作者也提到，在慢动态场景中无法为惯导参数提供较好的观测，初始化在15s内无法达到良好的收敛，为了增强此种场景下的鲁棒性，作者提出了一种基于修改的纯惯导优化的尺度优化技术scale refinement technique，考虑所有的关键帧，只对尺度和重力方向进行估计，如Fig.2（d）所示，值得注意的是，此种情况下，常数偏差的假设不再成立，而是在优化过程中使用从地图中获取的估计值并将其固定。该优化过程非常高效，在局部制图线程中每10s进行一次，直到地图包含超过100个关键帧或者距离初始化超过75s。

5.3 Tracking and Mapping

跟踪线程解决简单的VI 优化问题：只优化最后两帧的状态，且保持地图点固定。

地图线程为了避免过大地图造成的问题，只对滑动窗口内的关键帧和地图点进行优化，当然也包括共视关键帧中的观测，但不对这些共视关键帧的位姿进行优化。

5.4 Robustness to Tracking Loss

在纯视觉SLAM 或 VO 中，遮挡物与快速运动会导致跟踪失败，ORB-SLAM 使用基于词袋库的重定位方法来解决该问题，但在部分EuRoC 数据集场景中无法完全解决该问题。本文提出的VI 系统会在跟踪少于15个地图点的情况下进入视觉跟踪失败状态，并通过以下步骤继续实现鲁棒定位：

  1. 短期跟踪失败：使用IMU 观测估计位姿信息，在一个大图像窗口内搜寻匹配地图点，然后进行VI 优化；若超过5s未成功，进入下一步骤。
  2. 长期跟踪失败：初始化一个新的VI 地图，并将该地图设为活动地图。

6 Map Merging and Loop Closing

为了避免false positive回环检测，DBoW2 进行时间和几何一致性检查，使得回环检测的准确率可达100%，但召回率只有30%-40%。而且，时间一致性检查太耗时间，作者发现在Atlas 中使用这种回环检测方法会导致频繁的延迟与低召回率。

为解决该问题，作者提出了一种新的地点识别算法，该算法有两个创新点：

  1. 当制图线程插入一个新的关键帧时，与Atlas 中现有的所有关键帧进行匹配，如果匹配关键帧属于活动地图，则进行回环检测；否则，将匹配关键帧所属的地图与活动地图进行地图融合。
  2. 此外，得到匹配关键帧后，将匹配关键帧对及其共视图中的邻居构建为一个局部窗口，在窗口内进行中期数据关联，以提高回环检测和地图融合的精度。

6.1 Place Recognition

地点重识别的步骤：

  1. DBoW2 候选关键帧：在Atlas DBoW2 数据库中搜寻当前关键帧 $K_a$ 的三个最相似的候选关键帧 $K_m$ ，注意，这里不包括该关键帧的共视帧；
  2. 局部窗口：对于每个 $K_m$ ，构建一个局部窗口包含 $K_m$ 、共视关键帧以及观测到的地图点；然后根据DBoW2 建立 $K_a$ 与局部窗口内的假定地图点匹配。
  3. 3D 对齐转换：利用RANSAC 算法，根据匹配点解算位姿转换矩阵 $\mathbf{T}_{am}$ ，对于纯单目或单目-惯导未构建成熟地图的情况，计算相似转换 Sim(3)，否则计算 SE(3)。
  4. 匹配细调：根据解算的 $\mathbf{T}_{am}$ 搜寻当前关键帧 $K_a$ 与局部窗口内所有地图点的匹配，在此基础上进行双向重投影误差非线性优化；如果内点数量超过一定阈值，则在更小图片窗口内进行第二次细调。
  5. 三个共视关键帧的验证：DBoW2 回环检测的时间一致性检验需检验连续三个关键帧，会造成延迟或遗漏地点识别；作者认为，大部分情况下验证所需的信息已经存在于地图中，可在活动地图中搜寻与 $K_a$ 相匹配的两个关键帧（超过一定匹配地图点数），然后使用这两个关键帧来验证 $\mathbf{T}_{am}$ 。
  6. VI 重力方向验证：在VI 中，若地图已经构建成熟，可获得 $\mathbf{T}_{am}\in SE(3)$ ，然后进一步检验pitch、roll角度是否在设定阈值下来确定地点识别假设是否成立。

6.2 Visual Map Merging

融合过程如下所示：

  1. Welding window assembly：该融合窗口包含 $K_a$、$K_m$ 、它们的共视关键帧以及所有的观测地图点，属于 $M_a$ 的所有关键帧和地图点通过 $\mathbf{T}_{ma}$ 与 $M_m$ 进行对齐。
  2. Merging maps：$M_a$、$M_m$融合起来变成新的活动地图，然后对重复地图点进行清除，对共视图、essential 图进行更新。
  3. Welding bundle adjustment：在窗口内对所有的关键帧进行局部BA 优化，如Fig.3（a）所示。
  4. Essential-graph optimization：地图融合之后，使用essential 图进行基于因子图的优化，在此过程中welding 窗口内的关键帧位姿保持固定；经过优化，welding窗口内的位姿矫正信息会进一步传递到剩余地图中。

fig3

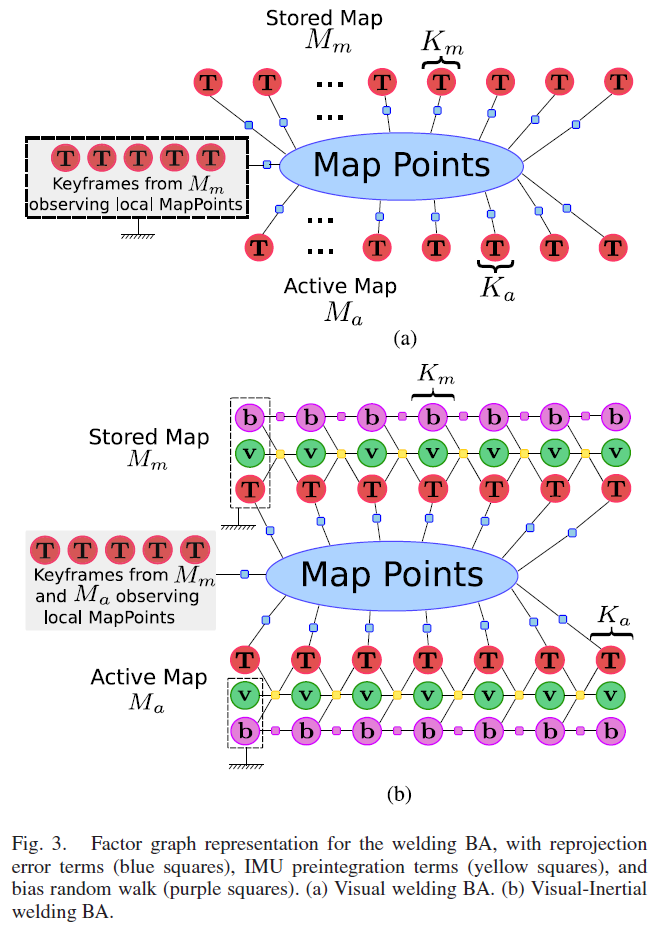
6.3 Visual-Inertial Map Merging

VI 地图融合较纯视觉有部分改变，在步骤1和3中进行了以下调整：

  1. VI welding window assembly：$\mathbf{T}_{ma}$ 会根据地图是否成熟分别选用SE(3), Sim(3)。
  2. VI welding bundle adjustment：对位姿、速度、 $K_a$ 和 $K_m$ 的IMU 偏差，以及之前的5个关键帧进行优化，如Fig.3（b）所示，除了关键帧位姿，所有的观测地图点也进行优化。

7 Experimental Results

作者在EuRoC 数据集上进行测试，取十次实验结果中的中位数与SOTA 算法进行比较，结果如表2所示：

t2

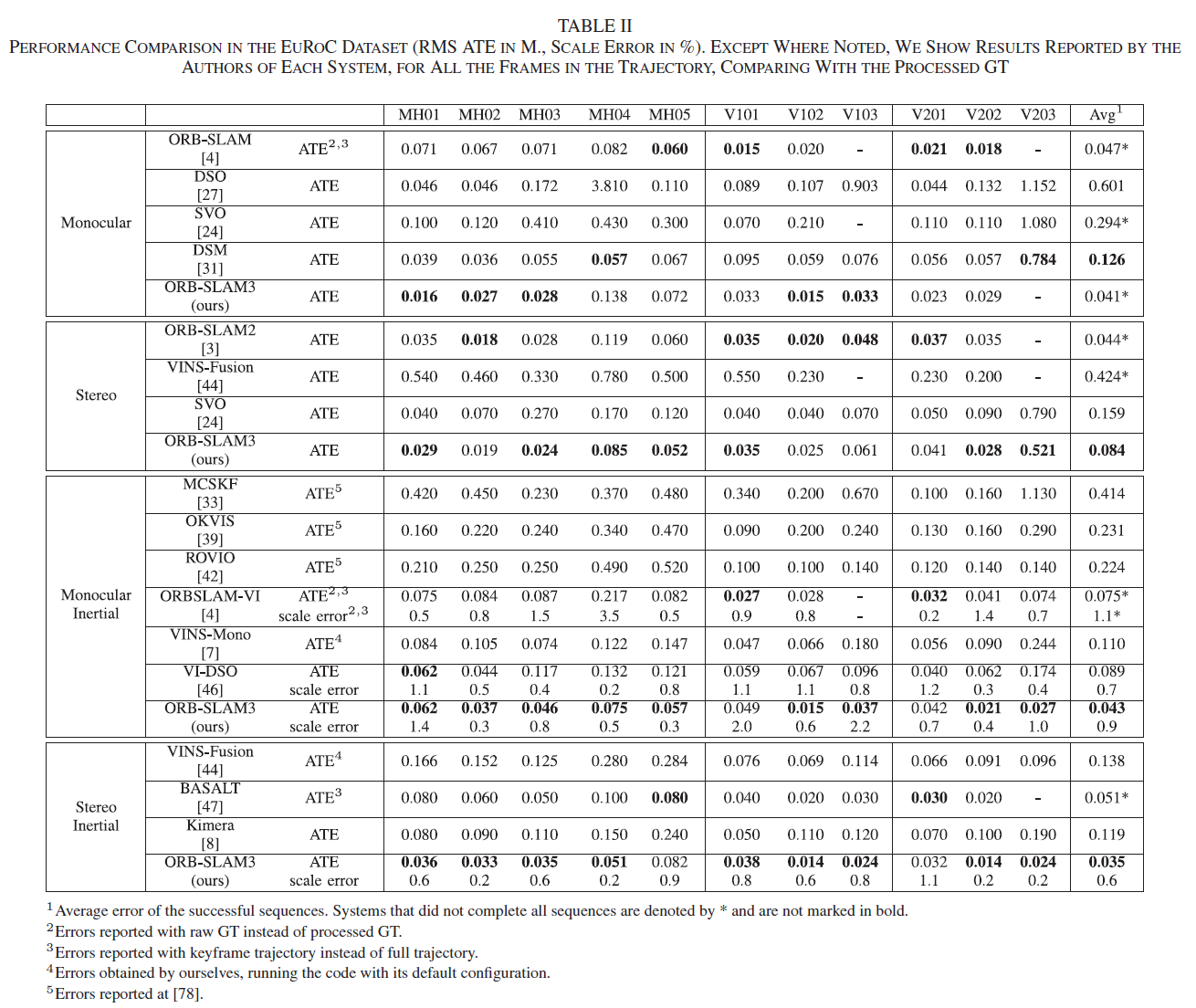
上表结果可证明本系统的优越性，特别是VI 系统的优势更为明显；但是，作者也指出双目-惯导较单目-惯导的优势很小，特别是在困难场景V203中，作者总结为加入惯导不仅提高了精度，减少了ATE 误差，而且也极大增强了系统的鲁棒性。

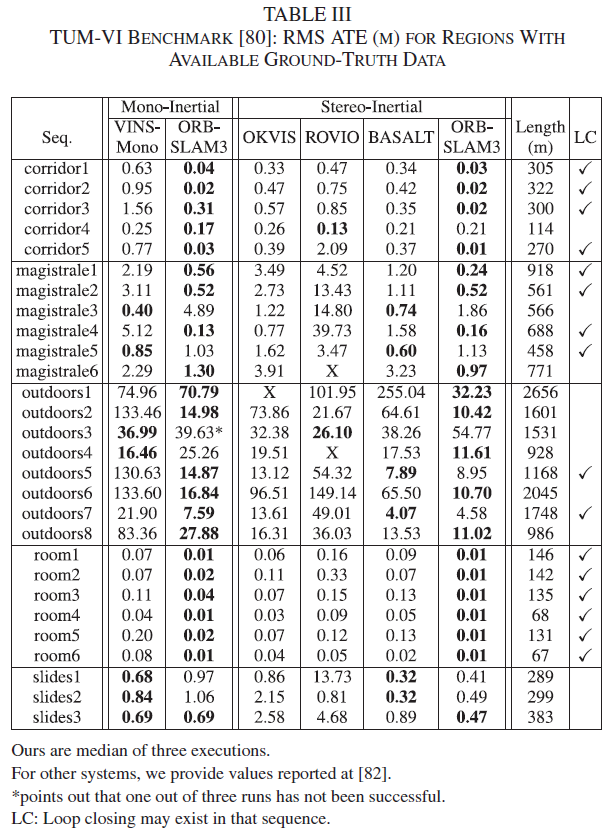
TUM-VI 数据集上的测试结果如表3所示，可以清楚看出本系统在单目-惯导、双目-惯导上的优势。

t3