Hsu, Li-Ta. “Analysis and Modeling GPS NLOS Effect in Highly Urbanized Area.” GPS Solutions 22, no. 1 (November 4, 2017): 7. https://doi.org/10.1007/s10291-017-0667-9.
1 Introduction
传统的基于测距的NLOS探测矫正方法难以适用于低成本接收器的原因在于:
- 利用ray-tracing 的计算成本太高;
- 3D 建筑模型难以实时获取到。
本文的创新与贡献在于提出一个应用于低成本设备中用于基于假设定位 hypothesis-based positioning 的NLOS 模型,而不需要使用ray-tracing。
在分析阶段,利用给定的接收机位置真值和3D 建筑模型进行NLOS 识别,也就是说,如果ray-tracing 模拟表明建筑模型挡到了信号的直线传播,但是接收机仍然接收到了该卫星的信号,那么就认定该信号为NLOS 信号。为了获取伪距NLOS 信号延迟,利用差分GPS 对其他误差进行消除;在城市环境中采集24h 的GPS 原始数据来恢复不同载噪比、不同高度角的NLOS 信号伪距误差。作者发现,NLOS 信号造成的伪距误差与卫星的高度角高度相关,而不是载噪比。最终,作者构建了一个关于卫星高度角和接收机与反射建筑物之间距离的方程来作为NLOS 延迟模型。
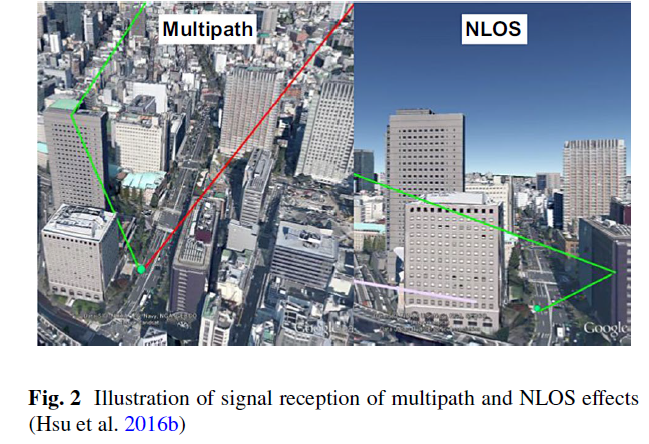
2 Estimation of NLOS delays in the pseudorange domain
伪距测量的误差项包括电离层延迟、对流层延迟、卫星钟差、轨道误差、接收机钟差以及我们的目标NLOS,其他误差需要在NLOS 分析前进行消除,本文分别使用 DGPS 和 最小二乘法(LSE)来处理前部和后部误差。
2.1 Differential GPS correction
参考站的多路径、NLOS 效应可以忽略,因为参考站一般选取安置在开阔环境中,且使用带有扼流圈的接收天线。理论上来讲,若流动站和参考站之间的距离小于100 km时,DGPS 矫正参数可以消除卫星钟差、轨道误差、电离层对流层延迟。
2.2 Receiver clock bias and thermal noise
接收机钟差的消除是通过将其视为未知数,利用多个伪距观测连同位置参数一同解算来获取的。为了更好地计算接收机钟差可以将位置参数从求解方程中进行剔除,作者利用香港的精细地形图(分辨率20 cm)等手段来获取接收机的精确静态位置,从而实现对位置参数的消除,进而利用伪距观测来计算接收机钟差。为了进一步提高对接收机钟差的解算精度,作者利用载噪比和ray-tracing 方法对NLOS 信号进行简单地识别,只利用LOS 信号对接收机钟差进行解算。
接收机热噪声误差被忽略掉,因为其远小于NLOS 带来的影响。
最终,NLOS 信号带来的延迟被定义为:
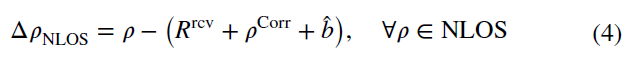
其中,$\rho$ 表示NLOS 伪距测量值;$R^{rcv}$ 表示卫星与接收机之间的LOS 距离;$\rho^{Coor}$ 表示DGPS 矫正参数。
3 NLOS data analysis
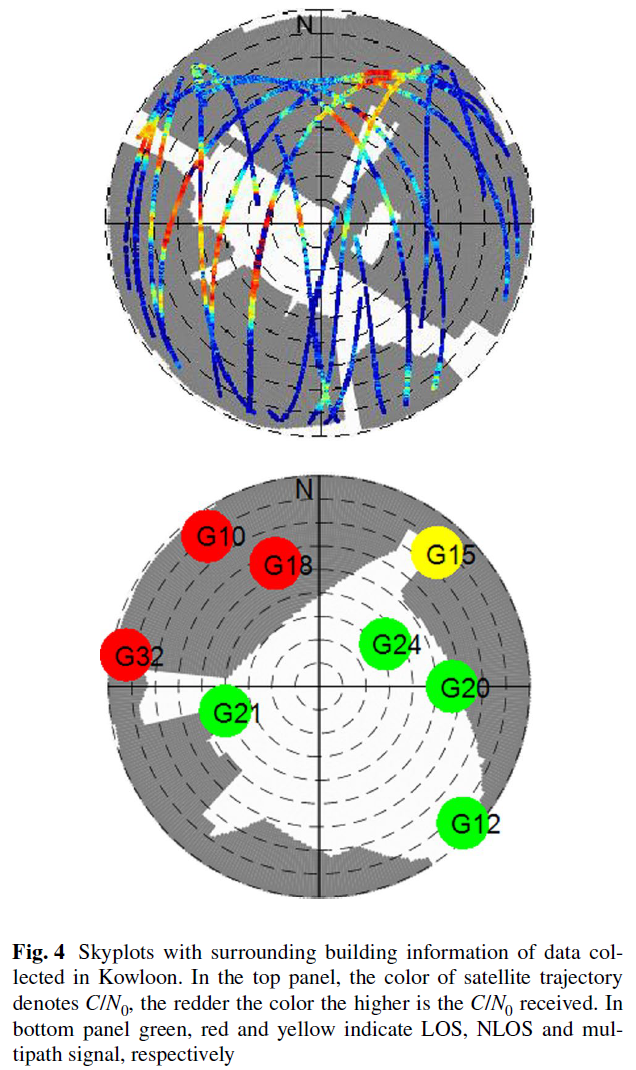
一个level of detai (LOD) 1 的3D 建筑模型从香港地政总署获取,在香港九龙的不同地方采集到了两份数据,数据一与数据二分别包含24 h 以及 30 min 的GPS 伪距原始观测量,两份数据的天空视图如Fig. 4所示。
3.1 NLOS data 1:case of 24 h
24 h 的观测数据中一共有128,054个NLOS 观测数据,Fig. 5展示了NLOS 信号伪距延迟直方图。
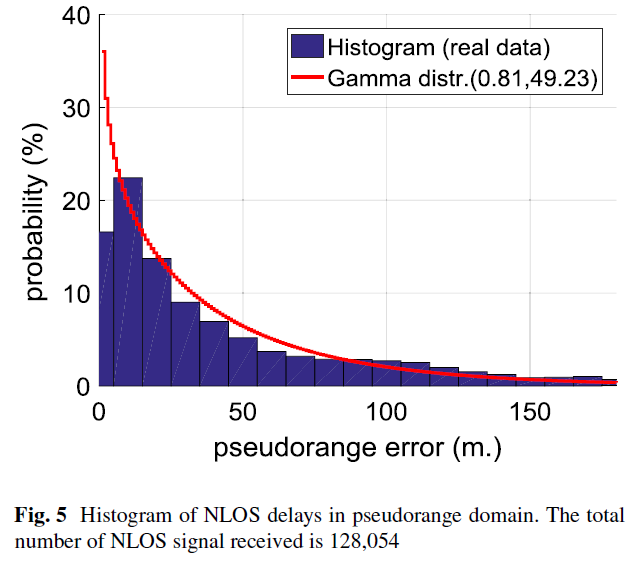
作者对该NLOS 误差概率分布利用Gamma 分布进行拟合:
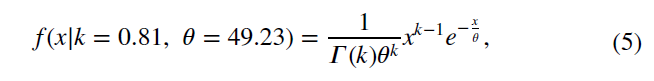
根据传统的定权模型,信号强度表明了伪距测量的质量,Fig. 6展示了NLOS 延迟与载噪比之间的关系,观察该图可以发现,随着载噪比的增加,NLOS 误差会缓慢下降,其标准差也有相同的趋势。这表明利用信号载噪比对GPS 观测进行定权确实可在一定程度上提高定位结果。
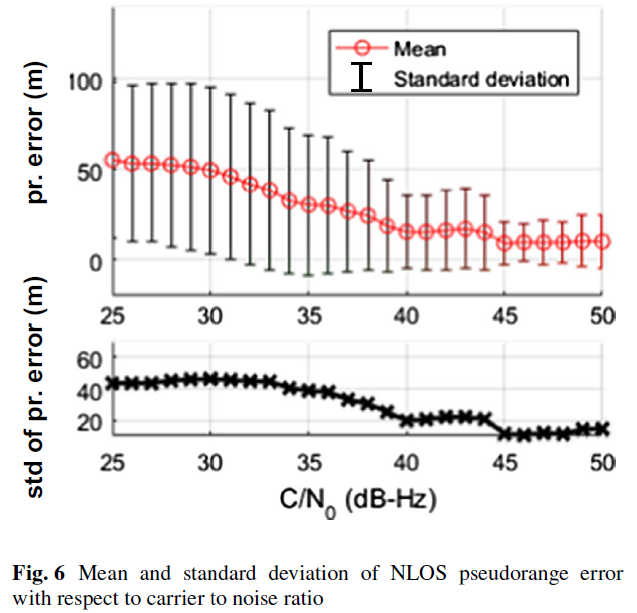
在传统的基于高度角的定权模型中,一些误差源(如大气误差、多路径误差等)与卫星高度角相关,这些误差通常随着高度角降低而单调增加。Fig. 7展示了NLOS 延迟与高度角之间的对应关系,由图可直观看出NLOS 延迟与高度角有明显的负相关关系,这说明传统的高度角定权模型也可用于消除NLOS 效应。
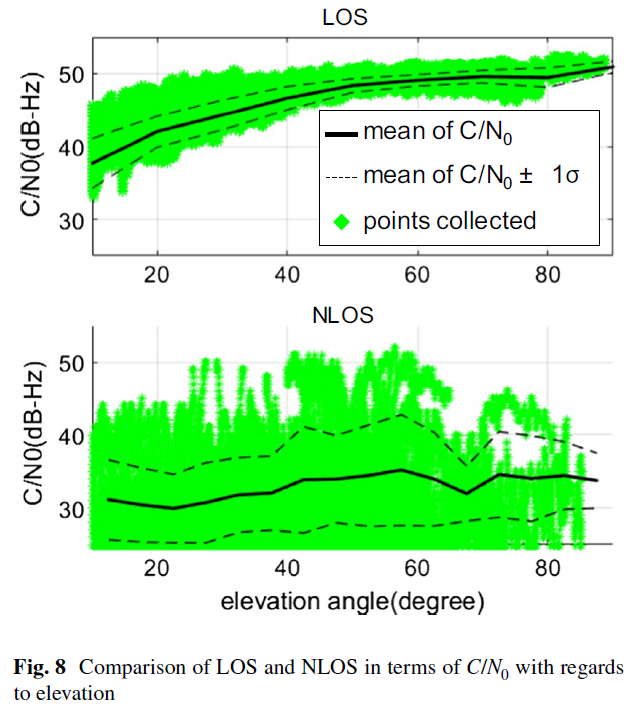
Fig .8展示了使用相同接收机接收到的LOS/NLOS 信号的不同表现。对于LOS 信号,高度角越高,载噪比均值越大、标准差越小,这说明对于LOS信号而言,高度角越高质量越稳定。然而,NLOS 信号却不同,随着高度角的增加,载噪比均值与标准差均没有明显的改善,这是因为NLOS 信号是反射信号,反射表面的材料会严重影响信号的强度。比较Fig .8 的上下两图,发现也许可以利用信号在不同高度角下的载噪比变化来区分LOS/NLOS 信号。
3.2 NLOS data 2:case of 30 min
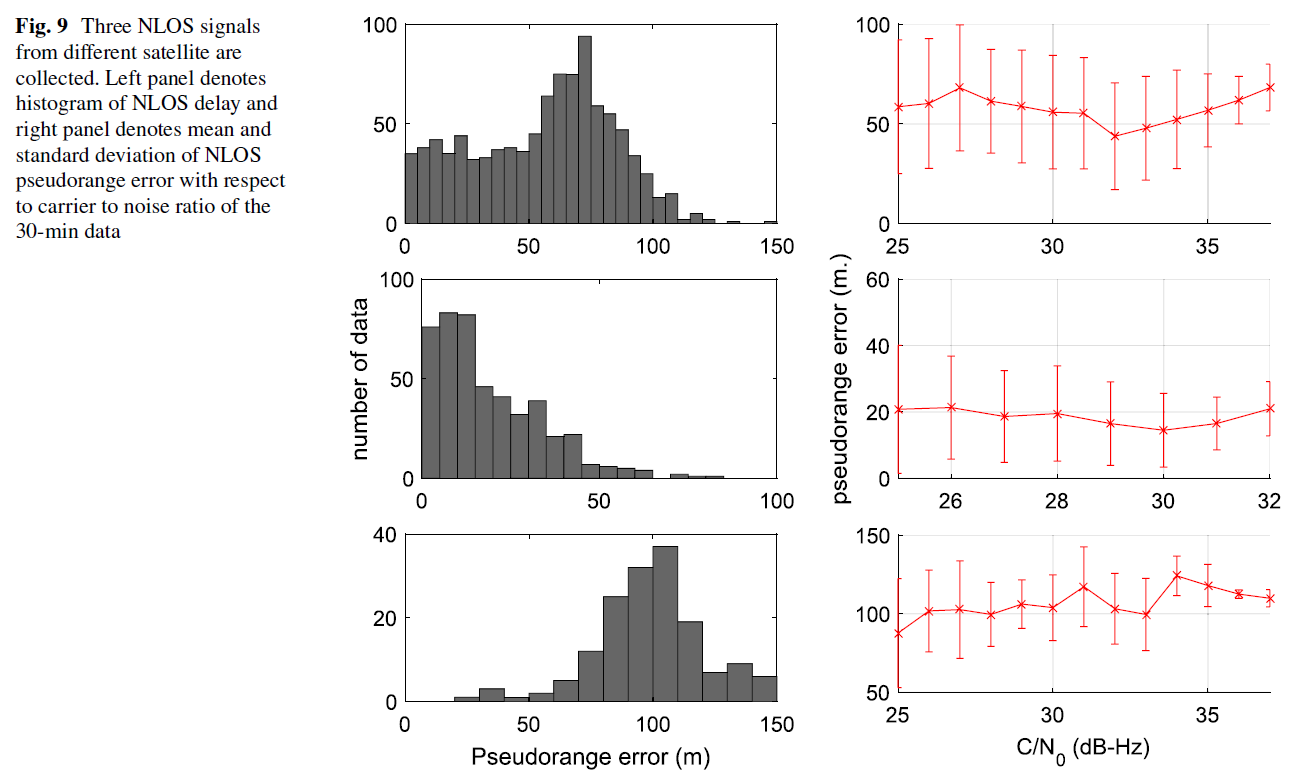
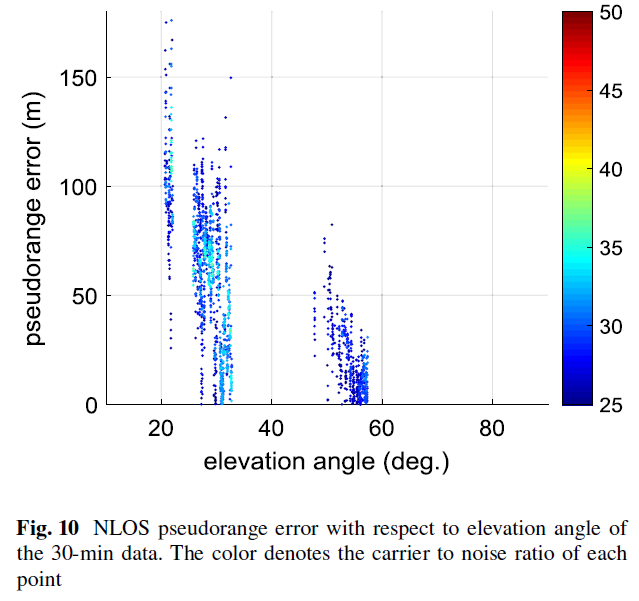
如Fig. 9,Fig. 10 所示,NLOS 伪距延迟并不会随着载噪比的增加而有明显的下降,但是会随着高度角的增加而明显下降。由于NLOS 信号可以一直存在于环境中,其载噪比也可以很强,所以无法利用载噪比来判断LOS/NLOS 信号。上节提到的载噪比与NLOS 延迟之间存在一定的相关关系(Fig. 6),这是因为高度角与载噪比之间的关系造成的:高度角增加,载噪比也会增加。
综上所述,作者认为高度角是NLOS 伪距误差的主导因素。
4 Modeling of NLOS
作者考虑现代城市环境中,建筑表面多使用玻璃作为外表材料,因此GPS 信号的反射遵循反射定律,如Fig. 11所示。
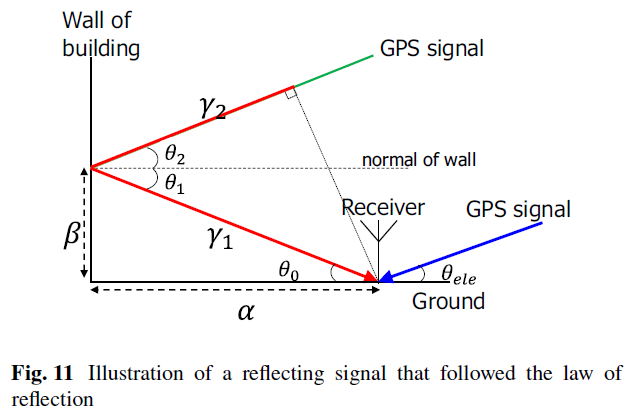
由于卫星距离接收机的距离远大于LOS 与反射信号之间的距离,因此可以认为蓝色的LOS 线不仅与绿色线平行,而且距离相等。因此,NLOS 延迟 $\gamma$ 可表示为:

其中,$\alpha$ 表示接收机与反射信号的遮挡物之间的距离;$\theta_{ele}$ 表示卫星高度角。根据反射定理可以得到 $\theta_{ele}=\theta_2=\theta_1=\theta_0$ ,最终,NLOS 延迟 $\gamma$ 可表示为:
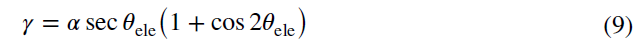
上式中,对与接收机而言只有距离参数 $\alpha$ 是未知的,可通过2D 地图或者LiDAR 进行获取。
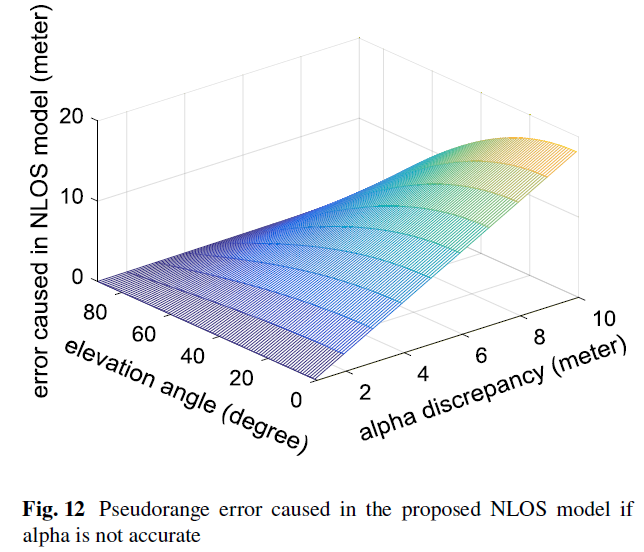
Fig. 12展示了卫星高度角以及距离参数 $\alpha$ 对NLOS 模型误差的影响。