Wu, Yanmin, Yunzhou Zhang, Delong Zhu, Yonghui Feng, Sonya Coleman, and Dermot Kerr. “EAO-SLAM: Monocular Semi-Dense Object SLAM Based on Ensemble Data Association.” In 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 4966–73. Las Vegas, NV, USA: IEEE, 2020. https://doi.org/10.1109/IROS45743.2020.9341757.
1 Introduction
作者认为object SLAM 当前面对两种问题:
- 在面对包含多个物体实例的复杂场景中,现有的DA 方法不够鲁棒或准确。
- 物体位姿估计不够准确,特别是对于单目object SLAM。
为此,作者提出了一个单目object SLAM 算法——EAO-SLAM,来解决DA 和位姿估计问题。
本文的贡献如下:
- 提出一种集合数据关联策略,可有效聚合不同的观测信息来提高DA 精度;
- 提出一种基于iForest (isolation forest) 的物体位姿估计架构,该架构对外点具有鲁棒性,可准确实现对物体位置、姿态及尺寸的估计;
- 基于提出的方法,应用EAO-SLAM 构建轻量级面向物体的语义地图;
- 在公开数据集和真实场景中进行测试,证明了本方法的有效性,代码开源:https://github.com/yanmin-wu/EAO-SLAM。
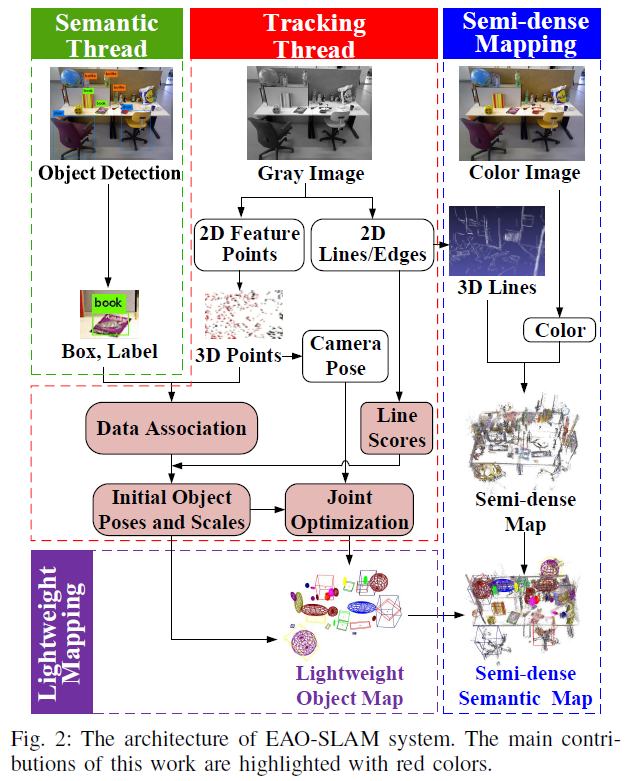
3 System Overview
系统整体架构如Fig.2所示,该算法是基于ORB-SLAM2 进一步开发的:
- 集合数据关联是在跟踪线程完成的,结合了bbox、语义标签和点云信息;
- 在DA 的基础上,使用iForest 来消除外点,并为联合优化提供准确的初始位姿估计;
- 然后对物体位姿与尺度、相机位姿进行联合优化,并构建一个轻量级物体语义地图;
- 最后,将该语义地图与半稠密地图进行结合,生成半稠密语义地图。
4 Ensemble Data Association
本文的标注:

4.1 Nonparametric Test
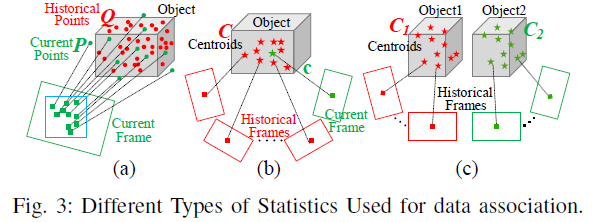
非参数测试是用来处理物体点云的(Fig.3 a中的红绿点),根据作者的实验研究(6.1节),这些点云不服从高斯分布。理论上讲,若P 和 Q 属于同一个物体,那么它们应该服从相同的分布,即 $f_P = f_Q$ ,接下来作者进行验证。
作者使用Mann-Whitney statistics:$W = min(W_P,W_Q)$ ,其中 $W_P,W_Q$ 定义如下:
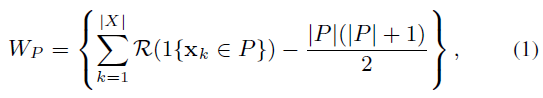
最终,作者证明如果两组点云 P、Q的Mann-Whitney statistics W满足式4,则证明这两组点云属于同一个物体,即标明DA 成功:
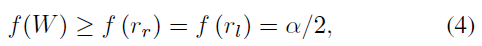
4.2 Single-sample and Double-sample T-test
单采样t-test 用于处理不同帧中观测到的物体中心(Fig.3 b 中的星形),被证明服从高斯分布(6.1节)。作者假设 $C, \mathbf{c}$ 来自同一物体,定义t:
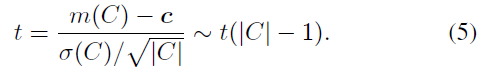
作者阐述,如果t 满足式6,则可证明假设成立,即 $C, \mathbf{c}$ 来自同一物体。
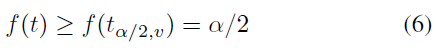
由于上述严格的DA 策略,以及较差的观测视角等情况,有可能将现有的物体判定为新物体,为此,作者提出了双采样t-test,通过对历史中心距离进行测试来判定是否需要融合两个物体(Fig.3 c)。为 $C_1, C_2$ 构建t:
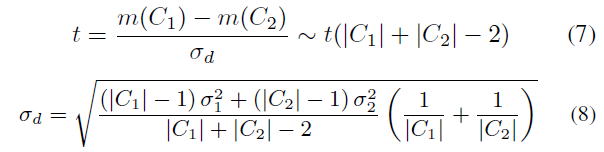
同样的,如果t 满足式6,则证明属于同一物体,进行融合。
5 Object SLAM
本节内容的标注:

5.1 Object Representation
作者使用立方体和二次曲面来表示物体:
- 对于常规形状的物体,如书、键盘、椅子等,作者使用立方体来表示(使用顶点 $P_O$ 进行编码);
- 对于没有具体方向的非常规物体,如球、瓶子等,作者使用二次曲面来表示(使用半轴 $Q_O$ 进行编码)。
立方体和二次曲面在世界坐标系中的表示为:
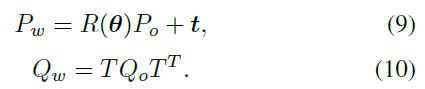
作者假设物体被放置在与地面平行的状态,即 $\theta_r = \theta_p = 0$ ,则对于立方体,只需要估计 $[\theta_y, \mathbf{t}, \mathbf{s}]$ ;对于二次曲面,只需要估计 $[ \mathbf{t}, \mathbf{s}]$ 。
5.2 Estimate t and s
基于iForest 的外点鲁棒的物体中心和尺度估计算法如下所示:

该算法的关键点在于:将数据点递归分为一系列孤立的数据点,将最容易被孤立出来的点视为外点。如Fig.4所示,d中的黄点经过4步被孤立出来,所以其步长为4,而e中的绿点步长为8,那么黄点更有可能是外点。
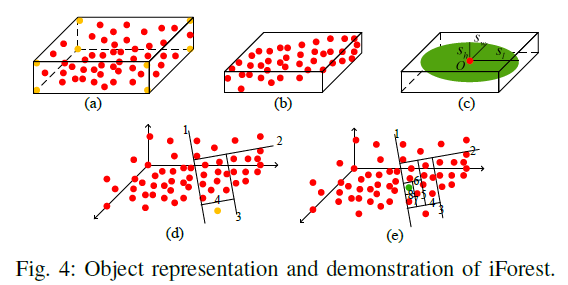
经过算法1,使用剩下的点计算 $\mathbf{t},\mathbf{s}$ ,基于 $\mathbf{s}$ 可在物体坐标系中初始化构建立方体和二次曲面,如Fig.4 a-c所示。 $\mathbf{s}$ 会与后续的物体和相机位姿得到进一步优化。
5.3 Estimate yaw angle
$\theta_y$ 的优化分为两步:首先找到一个良好的初始化值,然后基于初始化进行数次优化。位姿初始化过程如算法2所示:

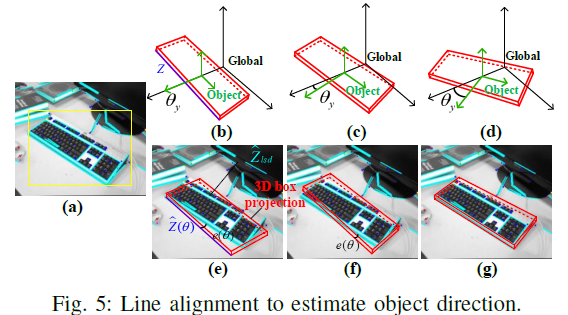
LSD 线段是从t 张连续图片中获取,位于bbox 内部的线段被分配给对应物体,如Fig.5 a所示。物体的初始姿态被假定为与全局坐标系保持一致,即 $\theta_0 =0$ (Fig.5 b),然后在 $[-\pi/2, \pi/2]$ 中均匀采样30个角度,针对每个采样角度,通过计算LSD 线段 $Z_{lsd}$ 和2D 投影边(由上步得到的立方体进行投影得到)之间的累积角度误差来得到该采样角度的得分,最终选取最高得分的角度作为初始值参与后续的联合优化。
5.4 Joint Optimization
利用初始估计进行联合优化:
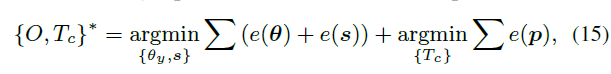
其中,$e(\theta)$ 为物体姿态误差,如Fig.5 e-g所示;$e(s)$ 定义为立方体投影边与最近的平行LSD 线段之间的距离;$e(p)$ 为传统SLAM 的重投影误差项。
6 Experimental Results
作者的实验包含以下部分:
- Distributions of Different Statistics
- Ensemble Data Association Experiments
- Qualitative Assessment of Object Pose Estimation
- Object-Oriented Map Building
本文算法着力于对物体位姿与尺寸进行估计,并构建半稠密物体级语义地图,没有对相机位姿解算效果进行介绍。