Liao, Ziwei, Wei Wang, Xianyu Qi, and Xiaoyu Zhang. “RGB-D Object SLAM Using Quadrics for Indoor Environments.” Sensors 20, no. 18 (January 2020): 5150. https://doi.org/10.3390/s20185150.
1 Introduction
本文的贡献:
- 提出了一种使用二次曲面作为物体模型的物体级SLAM 算法,并使用了两种RGB-D 二次曲面观测模型;
- 提出了一种从单张RGB-D 图片中提取出表示物体的完整椭球体的方法,该方法基于物体和其支撑平面之间的关系;
- 为二次曲面模型引进了一种非参数位姿图 nonparametric pose graph,来解决后端的语义数据关联问题;
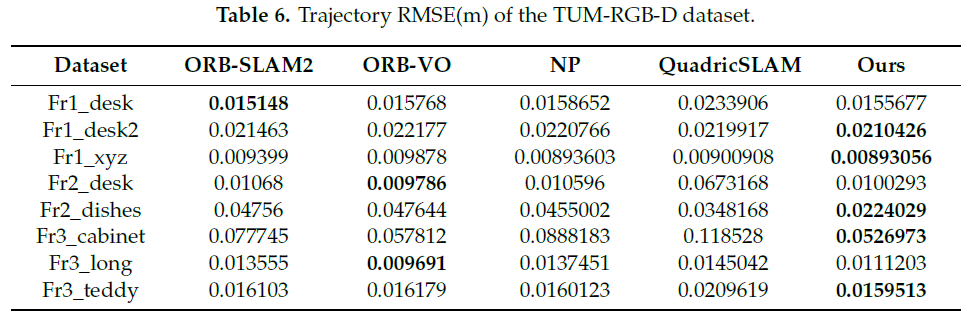
- 在两个公开数据集和自采数据集上,与两个SOTA 物体级SLAM 算法进行比较,评估了本算法的有效性。
3 Materials and Methods
3.1 System Overview
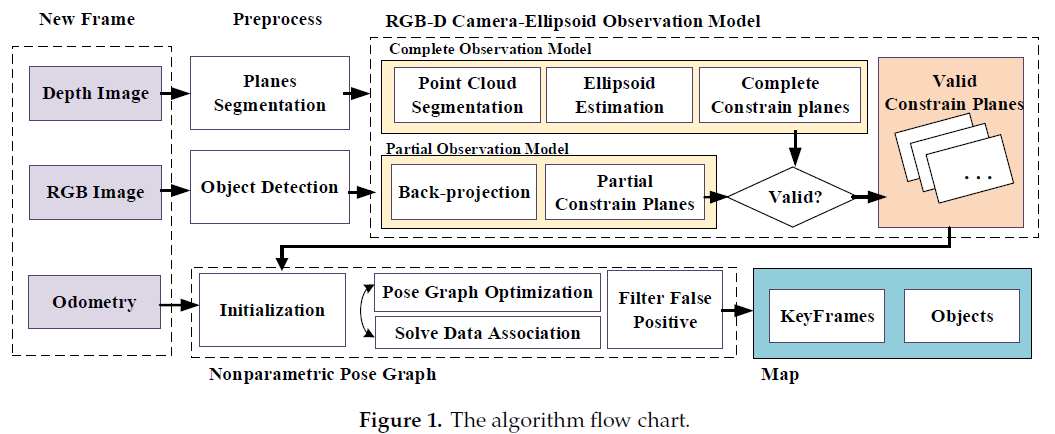
Fig. 1展示了本文方法的整体架构:
3.2 Quadrics Model
二次曲面包含多种类型,如椭球体、圆柱体等,考虑到室内人造物体多为闭合几何形状,作者使用椭球体作为物体的模型表示。
二次曲面可使用对偶形式 $\mathbf{Q}^\ast$ 来表示,对于任意切平面 $\pi$ 满足以下关系:

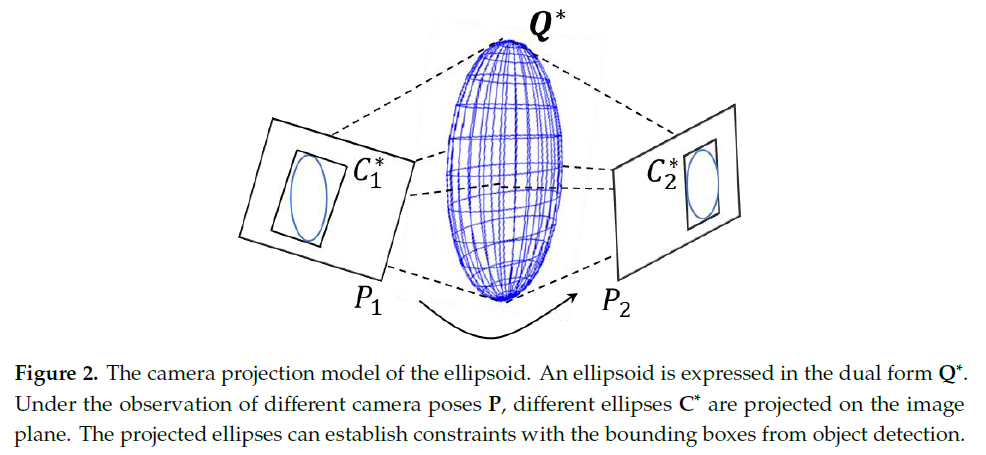
对偶二次曲面在相机观测 $\mathbf{P}$ 下得到曲线 $\mathbf{C}^\ast$ ,该过程如Fig. 2所示,并表示为下式:

其中,$\mathbf{P} = \mathbf{K}[\mathbf{R}|\mathbf{t}]$ 。
3.3 RGB-D Camera-Ellipsoid Observation Model
使用式2对椭球体进行投影映射为图像平面上的椭圆,结合物体检测bbox 构建约束,则单次观测只能包含4自由度的约束(bbox 4条边),因此,为了解算具有9自由度的椭球体,需要多次观测,且观测之间要有足够的视差。考虑到移动机器人的运动模式,其在垂直方向和pitch 方向的视角变化受限,容易造成unobservable 问题。
为解决该问题,作者使用RGB-D 相机提供的深度信息:从深度信息中提取物体的支撑平面,由此引入物体-平面的支撑关系来帮助分割物体点云,并估计物体的朝向信息。为解决多视角变化的需求,作者推导了RGB-D 完整观测模型,并使用单帧RGB-D 数据来估计完整的椭球体,以实现快速的初始化。针对物体遮挡导致的深度数据严重缺失问题,作者使用物体检测bbox 构建了部分约束模型,以实现对观测信息的最大化利用。
尽管RGB-D 观测可提供深度信息,但仍存在以下问题:1. 图像边缘造成的物体不完整;2. 物体间的遮挡;3. 光照、材料反射导致的深度信息不准确、不完整。这些问题会造成物体点云的缺失,对观测模型的构建造成影响。

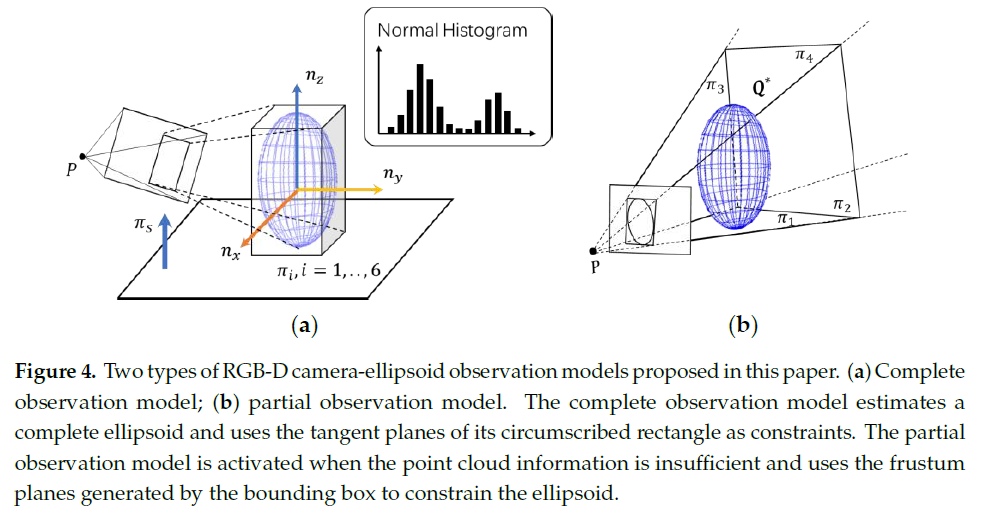
根据点云数据的完整度,作者提出了两种观测模型:部分约束模型和完整约束模型,如Fig. 4所示。
当点云质量较高时,使用完整约束模型从单帧RGB-D 图像中恢复完整的椭球体,该方法充分利用室内物体和其支撑平面之间的支撑关系来估计物体的位姿与形状;最终,该算法会为该椭球体建立一个约束立方体,立方体的6个面与该椭球体相切,从而获取至多9自由度的完整约束模型。
当出现严重遮挡或点云质量不足以构建一个完整的椭球体时,算法会使用部分约束模型,该方法充分利用bbox 产生的约束平面,并生成至多4个正切平面的约束。
此外,作者还提出了一种新颖的评估方式来判断立方体的质量,从而实现两种观测模型之间的灵活切换。
作者将提出的观测模型和评估方式应用至物体级语义SLAM 架构:
- 使用完整约束模型构建的椭球体来初始化新物体;
- 使用约束模型作为图优化中的损失函数,并解决数据关联问题。
3.4 Complete Constraint Model
完整约束模型充分利用人造物体的特性,以及它们与结构平面之间的关系;基于这些特性从单帧RGB-D 观测中恢复椭球体的完整参数,该过程如Fig. 5所示:
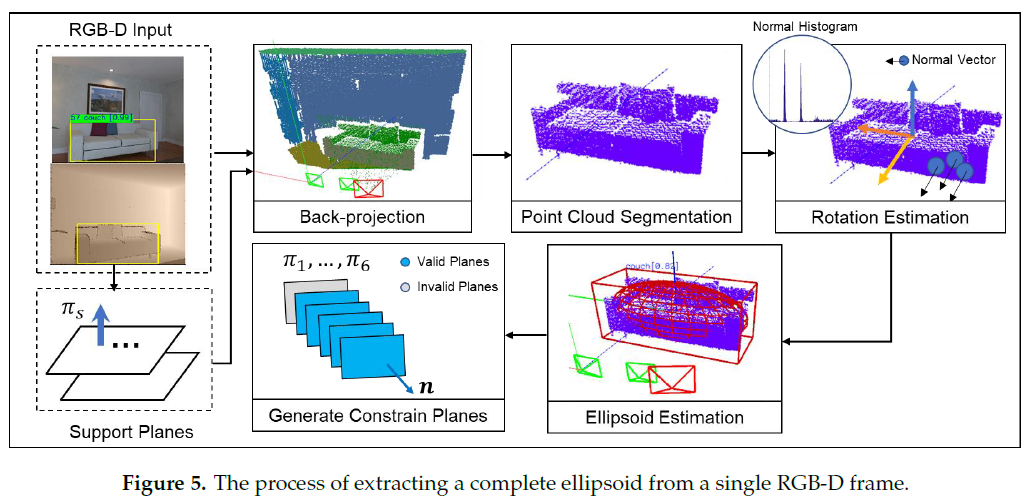
完成对椭球体的估计后,使用所提出的评估方式对椭球体进行评估:如果超过预设阈值,则保留该椭球体;否则切换至部分观测模型来实现对观测信息的最大化利用,并保留约束置信度。
3.4.1 Supporting Planes Segmentation
典型的人造室内场景有许多特性:存在大量平面,平面之间平行或正交,物体一般有对应的支撑平面。作者利用这些特性来辅助分割点云,并为椭球体旋转参数提供先验约束。

首先,基于作者之前的研究,使用RANSAC 方法从深度图像中提取平面,并记为平面集合 $S_0 = \{\pi_i\}$ ;这里作者使用了假设:物体的支撑平面与重力方向垂直,如地面、桌面等。然后,作者根据粗略估计的重力方向 $\mathbf{n}_g$ 选择潜在的支撑平面:认为机器人的支撑平面是地面,且RGB-D 相机在机器人上是固定的,则可从相机与机器人之间的转换矩阵中得到重力方向的粗略估计。根据重力方向与平面法向量之间的夹角,筛选出潜在支撑平面集合 $S = \{\pi_i\}$ 。
3.4.2 Object Point Cloud Segmentation
基于物体检测bbox,将深度图进行逆投影可以获取物体粗略的点云集合,然后,作者使用一个轻量级的分割方法获取更为精确的物体点云:使用Euclidean filtering 方法滤除属于支撑平面的点云,保留属于物体的点云 $\mathcal{C}_i$ 。
3.4.3 Object Orientation Estimation
作者提出一种基于物体和其支撑平面之间关系的物体朝向估计方法,该方法基于两个假设:1. 物体的主轴之一与支撑平面的法向量平行;2. 对于有着主朝向方向的人造物体,物体表面的法向量直方图可以反应这种方向趋势。
A Definition of object coordinate system
系统坐标系如Fig. 4(a)所示,Z 轴沿着重力方向向上,X 轴和 Y 轴表示物体两个正交的主方向。作者提到,由于椭球体是对称的,若沿着Z 轴每隔90度旋转四次,会得到四组旋转矩阵来表示椭球体的相同旋转。
B Z-axis estimation based on the supporting plane
室内场景下,物体的支撑平面基本是地面和桌面,这种情况下,物体和对应的支撑平面形成一种垂直关系,因此物体的Z 轴与支撑平面的法向量平行。在点云分割过程中,获取了物体支撑平面 $\pi_s$ ,据此可得到物体的Z 轴 $\mathbf{n}_s$ 。
C Y-axis estimation based on the histogram of normal vectors
如Fig. 7所示,大部分人造物体拥有互相垂直的主方向,如显示器、沙发等,对于这些物体,可以使用旋转作为角度约束信息;对于对称性物体,如水杯、瓶子等,方向信息对于这些物体没有意义。因此,作者根据物体语义标签来判断是否使用主方向来约束该物体。

对于有主方向的物体,作者取物体点云法向量集合中yaw 角直方图的峰值来作为该物体的Y 轴。首先,作者在支撑平面上搭建一个极坐标系统,取平面上一个单位向量 $\mathbf{n}_r$ 作为坐标轴。具体算法如下所示:
对于属于物体点云中的所有点 $\mathbf{P} \in \mathcal{C}_i$ 执行2-4步,通过将法向量投影至支撑平面来计算yaw 角;
根据局部深度信息来计算该点的法向量 $\mathbf{n}_p$ 。在提取平面的过程中,已经计算了整个深度图的法向量,所以可以直接获取该向量;
将法向量 $\mathbf{n}_p$ 投影至支撑平面 $\pi_s$ 来获取yaw 角。假设支撑平面的法向量为 $\mathbf{n}_s$ ,计算法向量 $\mathbf{n}_p$ 在平面上的投影向量 $\mathbf{n}_{ps}$ :

计算yaw 角 $\theta = acos(\mathbf{n}_{ps}, \mathbf{n}_r)$ ,将 $\theta$ 归一化至 $[0, \pi)$ 范围,并将 $\theta$ 添加至集合 Y中;
在获取所有点的法向量后,获取集合 Y 中的最大值,作为最终的 $\theta$ 值;
根据 $\theta$ 值计算相应的法向量形式 $\mathbf{n}_x$ —— 沿着平面法向量 $\mathbf{n}_s$ 将极坐标轴 $\mathbf{n}_r$ 旋转 $\theta$ 度:首先根据Rodriguez 公式计算旋转矩阵 $\mathbf{R}_{\theta}$ ,进而得到法向量 $\mathbf{n}_x$ 。
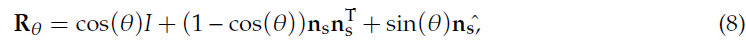

此外,基于该角度在集合直方图中的比例计算该置信度 $P_{rot}$ :

3.4.4 Ellipsoid Generation
根据物体的旋转矩阵 $\mathbf{R}_c$ 和物体点云,可以构建出点云的最小bounding 立方体。确定点云在三个主轴的半轴长 $\mathbf{s} = [a, b, c]^T$ ,取各轴的中心作为立方体的中心点 $\mathbf{t}_c$ ,进而得到该立方体的位姿:
对于任意立方体,均有其对应的内切椭球体。根据立方体主轴长度生成对角矩阵 $\mathbf{D} = diag(\mathbf{s})$ ,则该立方体的内切椭球体表示为:

由此,实现了从单帧RGB-D 提取了物体立方体模型。
3.4.5 Confidence Evaluation of the Complete Constraint Model
由于物体检测得到的bbox 是可靠的物体约束,所以,作者基于bbox 和完整约束模型构建的立方体来计算该模型的置信度。
首先,计算椭球体外形匹配概率 $P_{shape}$ ,根据式2将椭球体投影至图像平面中的椭圆形,在此基础上生成受限矩形;然后与bbox 计算IoU:
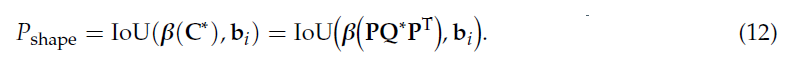
其中,$\beta(\mathbf{C}^\ast)$ 表示获取椭圆的外包矩形。
在此基础上,基于贝叶斯理论,结合物体检测概率 $P_{det}$ 、主方向估计概率 $P_{rot}$ ,得到该椭球体约束模型的置信度:

其中,$\alpha$ 为置信度阈值,判断当前模型是否可靠,若不可靠则选择使用部分约束模型。
3.4.6 Generate Constraint Planes
A Acquisition of tangent plane
为了灵活适应遮挡情况,作者将椭球体约束分割为多重离散约束。立方体的6个面均满足式1的正切约束,且满足角度约束:面的法向量与椭球体的某个主轴共线。因此,一个完整的约束平面包含两部分约束:正切约束和角度约束。整体的约束方程如下所示:
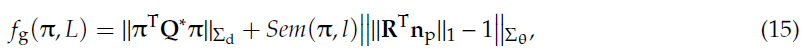
其中,$Sem(\pi, l)$ 用来判断物体是否有主方向,或切平面是否垂直于Z 轴。基于式15构建的完整约束包含6个约束平面和对应的角度约束。
B Occlusion of the image edges
因为使用了正切平面的形式来表示约束,所以可以判断每个正切平面的有效性,并移除由于遮挡造成的无效约束。每个正切平面包含受限矩形的4个顶点,作者通过判断位于图像边界内的投影顶点数量来决定该正切平面是否有效。
3.5 Partial Constraint Model
对于完整约束模型和部分约束模型,作者均采用约束平面来表示,以实现在图优化期间更好的收敛表现。
3.5.1 Acquisition of constraint planes
物体检测bbox 的每条边可通过逆投影形成一个平面:

其中,$\mathbf{P}$ 表示相机位姿;l 表示bbox 中的一个边。
3.5.2 Occlusion of the image edges
与完整约束模型类似,作者根据bbox 边与图像边界的距离来判断该边是否有效。有效边利用式18获取正切平面,进一步构建正切约束:

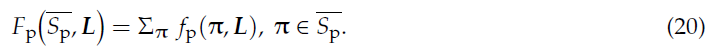
若所有的bbox 边均有效,则单帧图片可构建4自由度的约束,式19的约束方程与式15相比,缺少了角度约束。但由此完整约束模型和部分约束模型形成了统一的形式。
3.6 Object-Level SLAM
作者将未知的语义数据关联和物体语义标签作为离散随机变量添加进系统中,因此,系统变成了包含连续变量(相机位姿)和离散变量(数据关联、语义标签)的混合系统,使得位姿图优化传统的非线性优化方法失效;为此,作者提出了一种非参数化位姿图对该问题进行建模,并得到最优解。
3.6.1 Semantic Data Association
作者提到,不同于传统SLAM 中拥有众多的特征点,物体级SLAM 中只包含少量的物体,若发生DA 错误,则会对解算结果产生巨大影响;此外,同一类别的物体还会包含多个不同的个体,且常出现不同物体相隔较近甚至出现物体相接的情况。所以,在前端直接进行物体DA 比较困难。基于前人研究基础,作者进一步将二次曲面模型引进非参数化位姿图中来解决DA 问题。
3.7 Nonparametric Pose Graph
3.7.1 The Definition of a Nonparametric Pose Graph
在传统位姿图的基础上进行扩展,得到了如下式所示的联合优化问题:
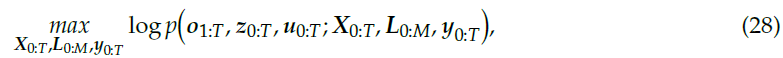
其中,$o,z$ 分别是里程计观测和地标观测;$\mathbf{X}, \mathbf{L}$ 分别是相机位姿与地标参数,$\mathbf{L}_i = \{\mathbf{Q}_i, l_i\}$ 包含物体的椭球体参数和语义标签;$u, y$ 分别是语义标签的观测和数据关联DA;物体个数M 是未知的,需要进行优化求解。
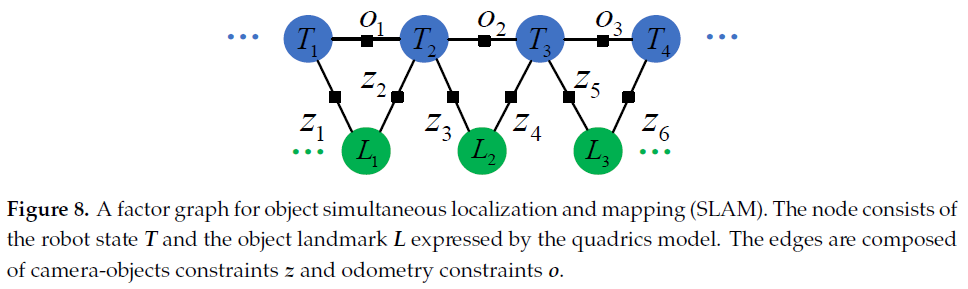
3.7.2 The Solution of a Nonparametric Pose Graph
前人使用 Dirichlet Process(DP)方法来计算非参数化位姿图,如Fig. 9所示,主要分为两步:
- 固定数据关联 y,利用最大似然法解算 $\mathbf{X}, \mathbf{L}$ ;
- 固定 $\mathbf{X}, \mathbf{L}$ ,利用最大似然法解算数据关联 y。
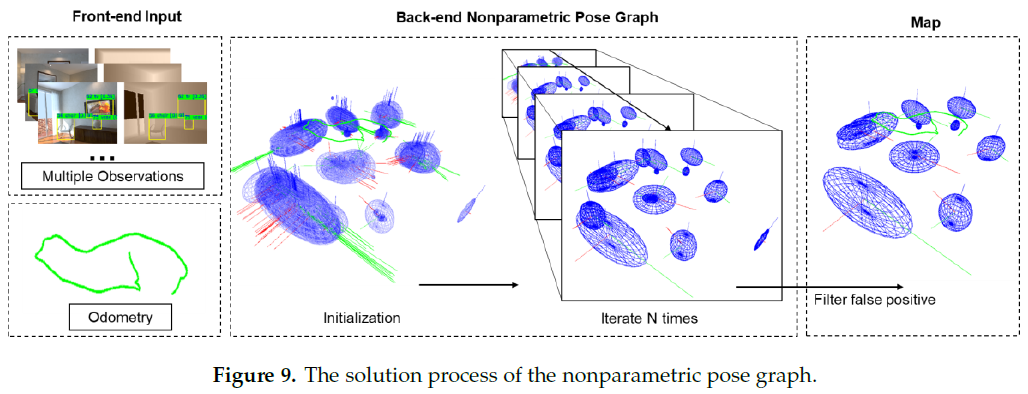
具体来讲,可分为以下步骤:
初始化:根据里程计数据初始化位姿 $\mathbf{X}$ ,将所有观测物体视为新物体来初始化物体地标 $\mathbf{L}$ ,初始化物体语义标签 $\beta_0$ ,然后重复执行2-4步直到收敛;
优化DA:固定 $\mathbf{X}, \mathbf{L},\beta$ ,使用下式更新数据关联 $y_t^k$ :
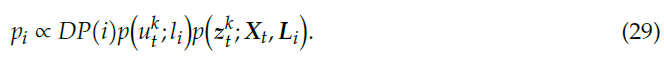
上式为DP 先验与观测似然的乘积;$p(u_t^k;l_i)$ 通过语义标签的数学模型来给定;$p(z_t^k;\mathbf{X}_t,\mathbf{L}_i)$ 通过二次曲面观测模型给定。然后使用最大似然确定数据关联 $y_t^k$ :

更新物体标签:固定数据关联 $y_t^k$ ,更新物体标签Dirichlet 分布的后验参数,直觉上讲,有最多观测次数的类别就是该物体的语义类别;
优化位姿与物体参数:固定DA $y_t^k$ ,解算 $\mathbf{X}, \mathbf{L}$ ,此处相当于传统的位姿图优化;
滤除false positive:对于观测次数少于设定阈值的物体,将其视为FP。
4 Experiment