Xiao, Zhongyang, Diange Yang, Tuopu Wen, Kun Jiang, and Ruidong Yan. “Monocular Localization with Vector HD Map (MLVHM): A Low-Cost Method for Commercial IVs.” Sensors 20, no. 7 (March 27, 2020): 1870. https://doi.org/10.3390/s20071870.
1 Introduction
本文的贡献:
- 提出一个基于语义向量提取和鲁棒地图匹配算法的低成本高精度定位算法;
- 提出一个基于滑动窗口的帧间运动融合(单目相机视觉里程计作为帧间约束)来有效提高定位的稳定性,特别是在稀疏定位特征的场景中也可以实现实时的稳定定位;
- 在真实世界中进行实验证明了精度与可靠性。
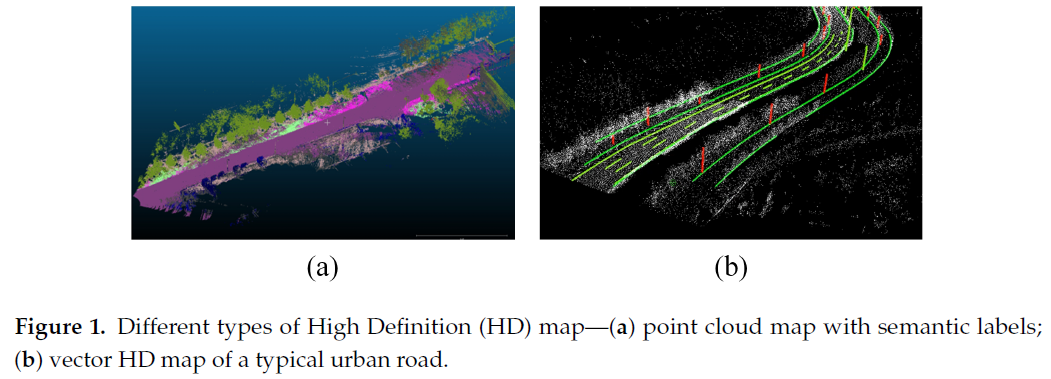
不同种类的高精度地图:
3 System Overview
MLVHM 系统概述如Fig. 2所示:
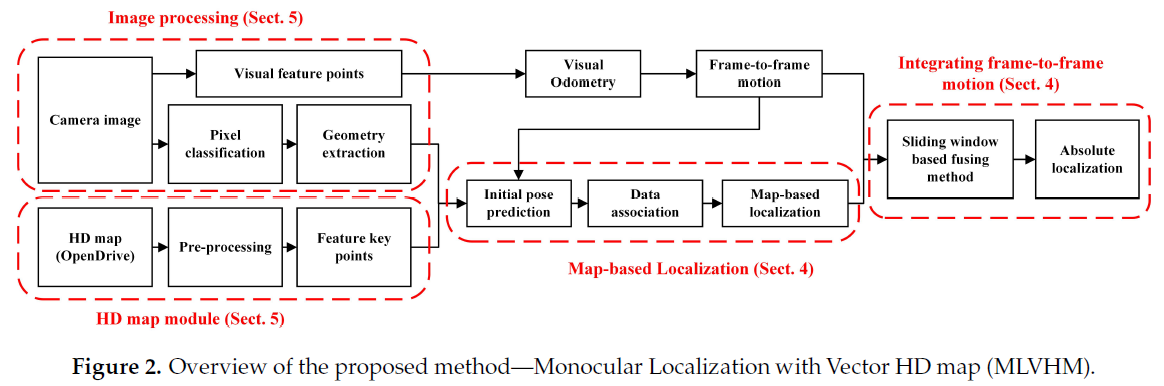
值得注意的是,ORB 特征只用来进行里程计计算作为帧间动作约束,并不参与地图匹配。
4 Map-Based Localization
4.1 Line-and Point-Based Camera Localization
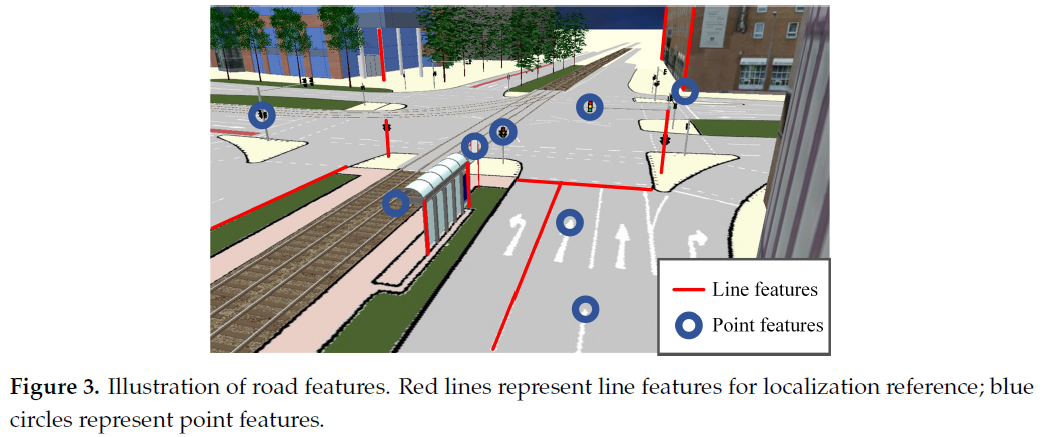
MLVHM 使用的是带有语义信息的几何特征,如Fig. 3所示,在Image processing 阶段,这些点与线特征被识别为带有语义信息,相应地,地图中的地标也是环境中关键元素的几何描述。
建立图片与地图间点、线特征的Mahalanobis 范数非线性优化:
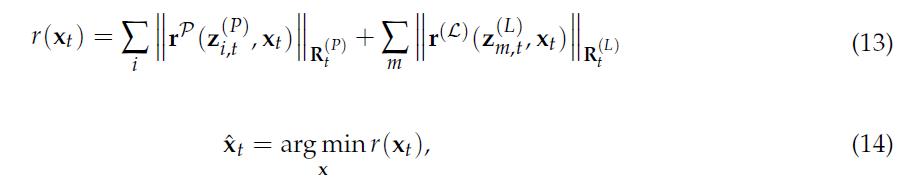
其中,$r^{\mathcal{P}}(z_{i,t}^{(P)},x_t),r^{\mathcal{L}}(z_{m,t}^{(L)},x_t)$ 分别是点与线的观测残差。如Fig. 4所示:
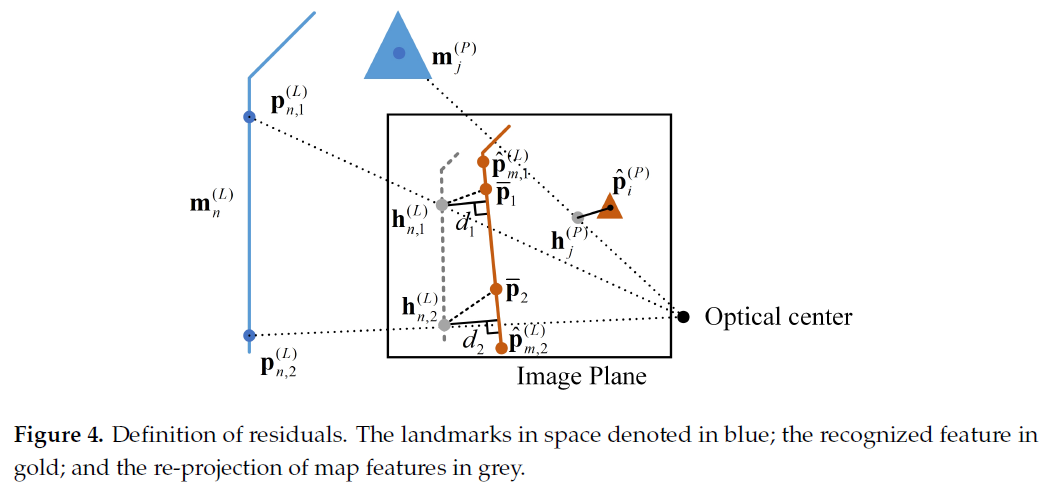
点特征的观测残差表示为 $r^{\mathcal{P}}(z_{i,t}^{(P)},x_t) = h_j^{(P)} - \hat{p}_i^{(P)}$ 。线特征两个端点的观测残差分别为 $r^{\mathcal{L}}(z_{m,t}^{(L)},x_t) = [d_1, d_2]^T$ 。
4.2 Data Association Method
作者采用一个RANSAC 升级版进行数据关联。
Basic RANSAC method
随机选取语义标签正确匹配的一组可能匹配点子集来评估该子集的质量,传统RANSAC 是通过测量内点的数量来评价子集的质量,即将地图投影到像素坐标系中,根据符合一定阈值内的匹配点数量来评判该子集的质量。
Improved RANSAC method
伪代码如Algorithm 1所示,$\mathbf{c}_{1-3}^{(L)}$ 表示选取三个(计算位姿的最小匹配数量)线匹配计算相机位姿 $\hat{\mathbf{x}}^{\ast}$ ,根据该相机位姿 $\hat{\mathbf{x}}^{\ast}$ 将地图投影到像素坐标系,计算内点(投影地标与图片特征小于阈值视为内点)集合 $\mathbf{c}^\ast$ 。此外,作者计算相机位姿 $\hat{\mathbf{x}}^{\ast}$ 与初始位姿估计 $\bar{\mathbf{p}}$ 之间的偏移量,若该偏移量小于 D,则将内点集合 $\mathbf{c}^\ast$ 并入关联集合 C 中(Algorithm 1:step 6)。
阈值 D 的设置是根据初始位姿估计 $\bar{\mathbf{p}}$ 的置信度来决定的,第一帧的初始位姿估计 $\bar{\mathbf{p}}$ 是通过低成本GNSS 接收机获取的,后续的初始位姿估计是结合上一帧的位姿与VO 进行估计的。
最终选取内点数最多的一组C 作为最终的数据关联结果。

4.3 Integrating Frame-to-Frame Motion
利用ORB-SLAM 算法计算帧间VO ,作为帧间运动约束实现对位姿估计的优化。
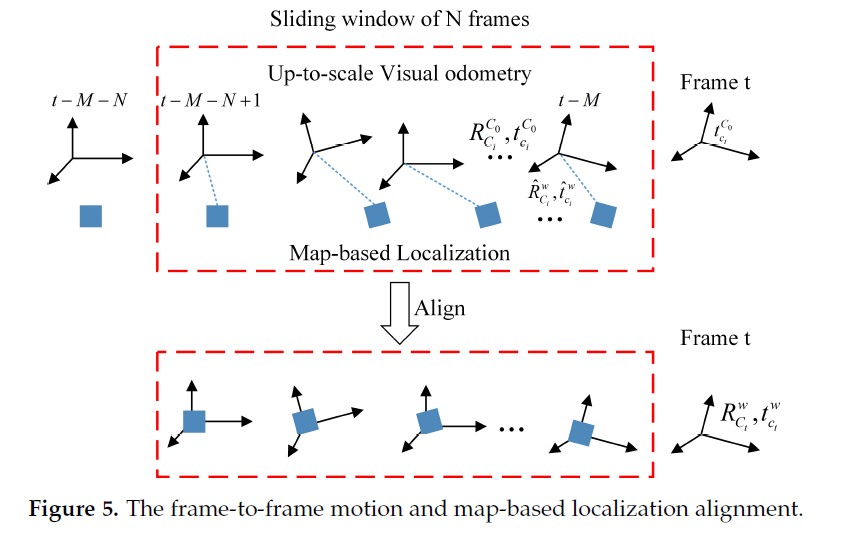
设定:帧 $c_i$ 较第一帧图像 $C_0$ 的位姿变换是 $\mathbf{R}_{c_i}^{C_0},\mathbf{t}_{c_i}^{C_0}$ ;由于单目相机的尺度不确定性,$\mathbf{t}_{c_i}^{C_0}$ 较真正的平移向量存在一个尺度因子 $s$ 的差距;相机坐标系与世界坐标系之间的转换关系为 $\mathbf{R}^{w}_{C_0},\mathbf{t}^{w}_{C_0}$ ;则相应的帧 $c_i$ 在世界坐标系下的位姿为:


由于语义分割消耗时间较久,故地图匹配的位姿结果通常与当前帧的时间不同,假定中间的延迟为M 帧。即假设当前时间为t,则距离最近的地图匹配位姿为 t-M 帧的结果,设定帧 $c_i$ 根据地图匹配求得的位姿为 $\mathbf{\hat{R}}_{c_i}^{w},\mathbf{\hat{t}}_{c_i}^{w}$ 。设定一个宽度为N 的滑动窗口对位姿进行优化,最终,使用帧间VO 约束的基于地图匹配的定位算法优化目标定义为:
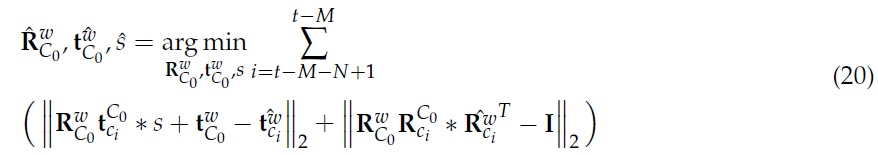
由此,可以得到帧t 对应的位姿:
