Hu, Xinggang, Yunzhou Zhang, Zhenzhong Cao, Rong Ma, Yanmin Wu, Zhiqiang Deng, and Wenkai Sun. “CFP-SLAM: A Real-Time Visual SLAM Based on Coarse-to-Fine Probability in Dynamic Environments.” In 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 4399–4406. Kyoto, Japan: IEEE, 2022. https://doi.org/10.1109/IROS47612.2022.9981826.
1 Introduction
作者认为当前面向动态场景的语义SLAM 方法虽然可以有效消除动态物体对位姿解算的影响,但很难实现精度与时间的平衡,难以实现实时处理,而且这些算法在低动态场景中的效果普遍不好。针对这些问题,作者提出了CFP-SLAM。
本文的贡献如下:
- 当使用DBSCAN 聚类算法来区分bbox 内的前景点和背景点,基于EKF 和 Hungarian 算法来补偿物体漏检测;
- 基于YOLOv5 和几何约束将物体的运动属性分为高动态和低动态,为后续的处理提供先验信息,以此来提高SLAM 系统的鲁棒性与适应能力;
- 提出一种基于物体静态概率的关键点静态概率两阶段计算方法,使用DBSCAN 聚类算法、对极几何约束以及投影约束来解决由非刚性物体局部运动造成的静态点误检测问题。
3 System Overview
3.2 System Architecture
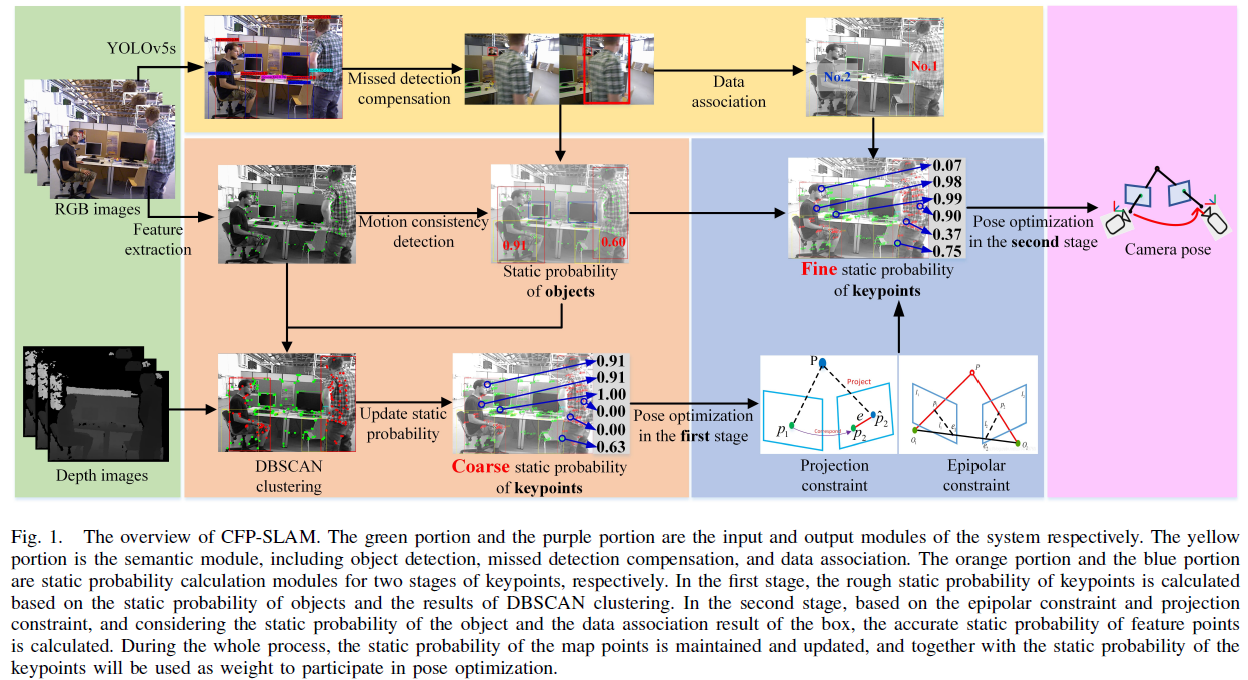
CFP-SLAM 系统架构如Fig. 1所示,该系统是基于ORB-SLAM2 开发实现的。
4 Specific Implementation
4.1 Missed Detection Compensation Algorithm
稳定准确的语义信息至关重要,漏检物体会带来以下影响:
- 影响后续基于语义先验信息处理动态物体的方法的正常运行;
- 在动态场景中,动态物体的突然出现会导致邻接帧之间错误匹配的特征点数量猛然提高,可能会导致SLAM 算法跟踪失败。
本系统使用EKF 和 Hungarian 算法来补偿潜在动态物体的漏检测:利用EKF 来预测当前帧中的潜在动态物体bbox,Hungarian 算法将EKF 预测的bbox 与YOLOv5 的检测结果进行关联,若预测框没有找到一个关联的检测框,则认为出现了漏检测,采用EKF 预测的框作为漏检测的框。然后,EKF 和Hungarian 算法进一步被用于帧间bbox 内的数据关联。
4.2 Static Probability of Objects
本系统提取并跟踪邻接帧之间的光流点对,并使用潜在动态物体bbox 外部的光流点对计算基础矩阵;然后计算光流点对的polar error,并使用卡方分布计算物体的静态概率;作者设定阈值为0.9,根据物体的静态概率分为高动态物体和低动态物体,然后将潜在动态物体bbox 内的所有特征点的静态概率初始化为物体的静态概率,图片中其余特征点的静态概率设置为1。
4.3 Static Probability of Keypoints in the First Stage
4.3.1 DBSCAN Density Clustering Algorithm
物体检测算法无法提供物体精确的掩码,特别是对于非刚性物体(如人类),检测框中会有很多的背景点。作者认为人表面上特征点的深度连续性很好,因此,作者使用DBSCAN 聚类算法来区分bbox 内的前景点和背景点,根据集群组的数量,作者将几组具有较小深度的集群组视为前景,该策略使得DBSCAN 聚类算法有着较强的鲁棒性。在识别出潜在动态物体bbox 内的前景点和背景点后,作者使用一个soft strategy 来进一步估计背景点的静态概率:
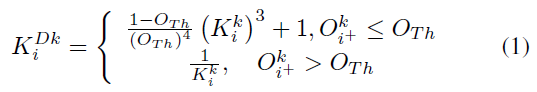
当前阶段特征点的静态概率还没有进行严格计算,属于比较粗糙的状态,此时的相机位姿估计容易受到动态点的影响,所以作者将此时高动态物体bbox 内前景点的静态概率设为0。
4.3.2 First Stage Pose Optimization
更新特征点的静态概率:
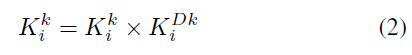
SLAM 系统初始化时,将地图点的静态概率初始化为对应特征点的静态概率;在初始化之后,帧间的位姿转换矩阵在第一阶段获取到,然后特征点的静态概率可进一步基于投影约束和对极约束实现精确计算。
4.4 Static Probability of Keypoints in the Second Stage
4.4.1 Static Probability Based on the Projection Constraints
利用初始位姿将上一帧的特征点投影至当前帧中,计算投影点至匹配点之间的欧氏距离,记为投影偏差距离 $d_i^T$ ;统计当前帧中动态物体bbox 外所有特征点的投影偏差距离并按从小到大进行排序,以0.8处的偏差距离作为自适应阈值 $d_{TH}^T$ ,同时记录最小值 $d_{min}^T$ ,作者使用Sigmoid 函数形式来计算bbox 内匹配点的静态概率:
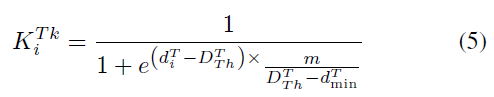
其中,参数 m 表示Sigmoid 函数的间隔。
对于一对匹配点,投影约束的满足不仅与静态环境的假设有关,也与位姿转换矩阵的求解正确与否有关。因此,作者计算位姿转换矩阵的统计置信度和计算置信度:
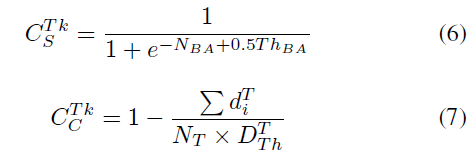
其中,$N_{BA}$ 为参与上帧位姿求解的内点数量;$Th_{BA}$ 为参与位姿解算的最小内点数量要求;$N_T$ 为所有采样点的数量;$\sum d_i^T$ 表示小于阈值的所有投影偏差距离之和。
4.4.2 Static Probability Based on the Epipolar Constraints
基于第一阶段的位姿估计,可以得到更为准确的基础矩阵:
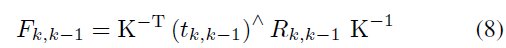
值得注意的是,上式的计算过程要求相机的平移应该要足够大,否则无法计算基础矩阵。由此,可以计算polar error:
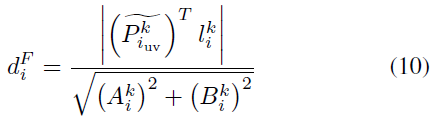
与上文类似的,可以基于对极约束计算相应的静态概率及置信度 $K_i^{Fk}, C_s^{Fk}, C_c^{Fk}$ ;若相机的平移未超过设定的阈值 $t_{Th}$ ,则有:
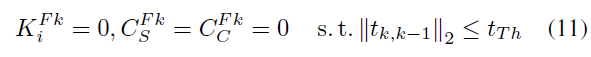
4.4.3 Second Stage Pose Optimization
在使用投影约束和对极几何约束后,更新当前帧与上一帧匹配点的静态概率;根据动态物体的移动概率,进行如下的特征点静态概率更新:
若物体静态概率低于阈值,则特征点静态概率更新为:
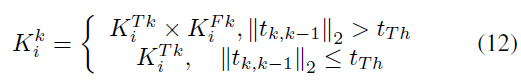
若物体静态概率高于阈值,则特征点静态概率更新为:
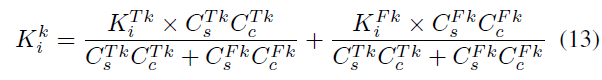
最后利用低动态特征点和地图点实现对相机位姿的第二次优化。
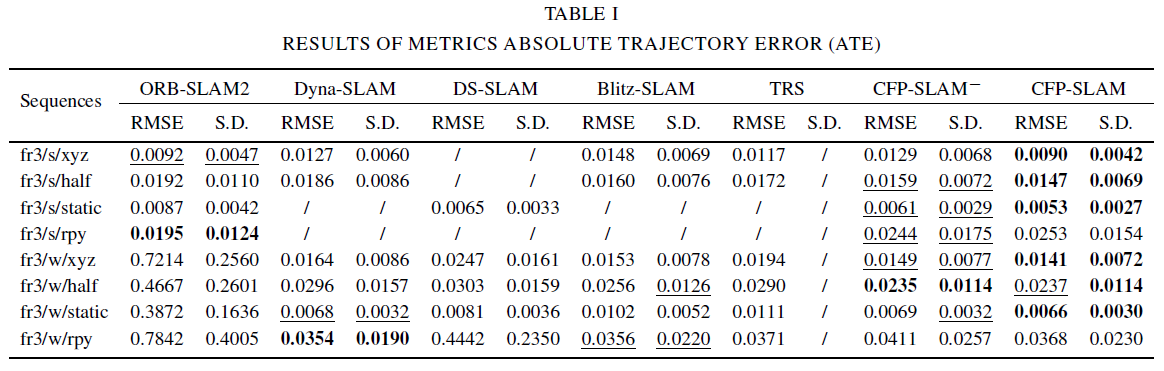
5 Experiments and Results