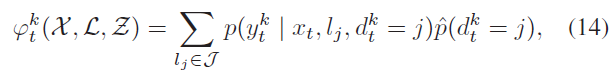Doherty, Kevin, Dehann Fourie, and John Leonard. “Multimodal Semantic SLAM with Probabilistic Data Association.” In 2019 International Conference on Robotics and Automation (ICRA), 2419–25. Montreal, QC, Canada: IEEE, 2019. https://doi.org/10.1109/ICRA.2019.8794244.
Abstract
语义SLAM 可被分解为:
- 一个离散的推理问题:决定物体种类与观测地标之间的联系(data association, DA)
- 一个连续的推理问题:获取机器人的位姿和地标的位置。
在模糊的DA 情况下,语义SLAM 通常不是一个高斯推理过程,现有的工作多是基于潜在的假设或者使用多重可能假设进行求解的。而作者提出了一种将DA 假设表示为一种等效非高斯模型的多模态形式的解算方法。
1 Introduction
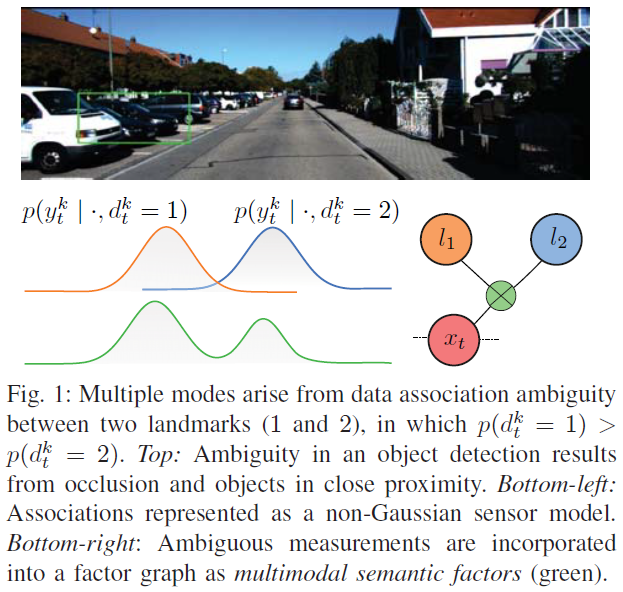
如图1所示,即便那些可以用高斯分布表示的观测模型在DA 和地标种类模糊的情况下也可以使用一个非高斯观测模型来表示。
本文做出的贡献:
- 提出一个nonparametric belief propagation 方法,为带有模糊DA 的语义SLAM 进行后验推理;
- 描述了multimodal semantic factors ,使得我们可以将不确定性包含到DA 和语义中,作为因子图中的非高斯因子,从而利用mm-iSAM (multimodal incremental smoothing and mapping) 进行位姿与地标的连续优化;
- 在仿真与真实数据集中进行实验,证明了该方法在DA 和地标种类模糊方面的鲁棒性。
3 Semantic SLAM with Ambiguous Data Association
3.1 Semantic SLAM with Known Data Association
本文使用最大后验估计理论进行求解:
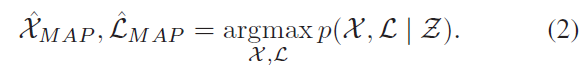
3.2 Probabilistic Data Association
为解决带有模糊DA 的语义SLAM 问题,作者分两步交替计算DA 概率与位姿、地标位置:
第一步,边缘化位姿与地标来计算DA 概率:
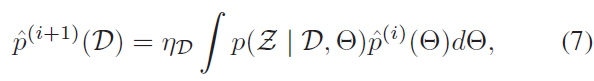
其中,$\eta_{\mathcal{D}}$ 为归一化常数;$\Theta = \{\mathcal{X}, \mathcal{L}\}$ 分别表示相机位姿与地标。
第二步,边缘化DA 来获取位姿与地标的分布:
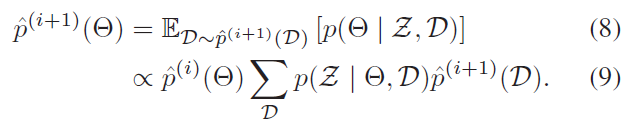
作者只在接收到观测之后进行一次迭代的DA 概率计算,从而减少了计算负担。
4 Multimodal Semantic SLAM
4.1 Multimodal iSAM
SLAM 中的因子图表示为:
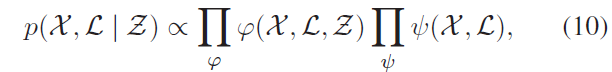
其中,$\varphi$ 表示观测因子,$\psi$ 表示先验因子。这里,因子图是一个间接的图模型,位姿与地标是被观测因子与先验因子连接起来的隐变量。每个变量的边缘分布可以使用belief propagation 进行解算,该方法在变量服从高斯分布时可以产生方便的分析形式。
multimodal iSAM 利用nonparametric belief propagation 来容纳非高斯变量,该方法在没有高斯假设的情况下,使用Gibbs 采样和kernel density estimation 组合方法来近似所有连续状态变量的置信度。对于随机变量X:
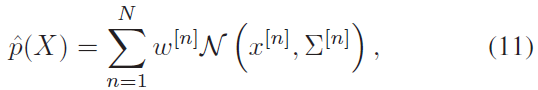
其中,$\mathcal{N}$ 是多元高斯核 multivariate Gaussian kernel,每个核的中心位于一个采样 $x^{[n]}$ , $w^{[n]}$ 是相应核的权重(采用均匀分布),而 $\sum^{[n]}$ 是相应高斯核的带宽,通过leave-one-out 交叉验证来获取。
该方法的一个好处在于,在后验估计中不再需要直接表示多种潜在可能的modes,这种隐含表示将推理的复杂度从假设数量中解耦了出来,因为在近似边缘化中的计算只依赖于采样的固定数量。结果就是,具有非常低概率的modes 在近似边缘分布中不太可能会出现,但是这些modes 也不会直接被舍弃,会继续存在于因子图中,这样那些后面变得更有可能的modes 可以得到恢复。
3.2 Multimodal Semantic Factors
设定一个语义观测模型因子为
$p(y_t^k | x_t, l_j) = p(y_t^{k,c} | l_j^c)p(y_t^{k,r} | x_t, l_j)p(y_t^{k,b} | x_t, l_j)$
其中,$y_t^{k,c}$ 表示路标类别,通过物体检测网络获取;$y_t^{k,r}$ 表示到路标的距离;$y_t^{k,b}$ 表示物体的方位。
假设 $p(y_t^{k,r} | x_t, l_j), p(y_t^{k,b} | x_t, l_j)$ 服从高斯分布,均值与方差分别为 $y_t^{k,r}$ ,$y_t^{k,b}$ 和 $\sigma_t^{2,k,r}, \sigma_t^{2,k,b}$ 。
假设一个统一的先验DA:
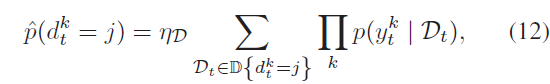
其中,$\mathbb{D}\{d_t^k = j\} = \{\mathcal{D}_t \in \mathbb{D}_t | d_t^k = j\}$ 表示在时间t 所有可能的数据关联集合,其中观测 k 与地标 j 相关联。
在给定数据关联 $d_t^k$ 情况下边缘化位姿估计、地标位置和种类,来计算每个观测 $y_t^k$ 的似然:
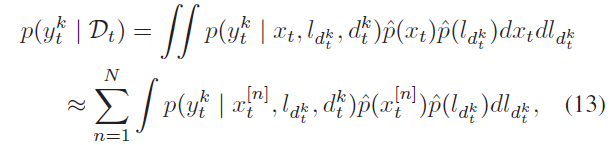
上式中,使用采样来逼近位姿分布上的积分计算,对于DA 计算,作者采纳了一个最大似然模型来简化地标位置的积分计算,作者发现该方法在高斯分布模型上效果很好,对于非高斯模型可以使用基于采样的逼近策略来近似。
对于属于集合 $\mathcal{J} \subseteq\mathcal{L}$ 中的所有地标 $l_j$ ,给定 $\hat{p}(d_t^k = j)$ ,一个multimodal 语义因子将位姿 $x_t$ 与 $\mathcal{J}$ 中的每一个候选联系起来: