Stenborg, Erik, Carl Toft, and Lars Hammarstrand. “Long-Term Visual Localization Using Semantically Segmented Images.” In 2018 IEEE International Conference on Robotics and Automation (ICRA), 6484–90. Brisbane, QLD: IEEE, 2018. https://doi.org/10.1109/ICRA.2018.8463150.
1 Introduction
本文利用近期在语义分割中的发展,设计了一个基于语义分割图片和语义点特征地图的定位算法,不再使用传统的描述子来描述特征,而是使用3D 位置坐标和语义标签来描述。
2 Problem Statement
2.1 Observations
坐标系与传感器安装位置如Fig 2所示:
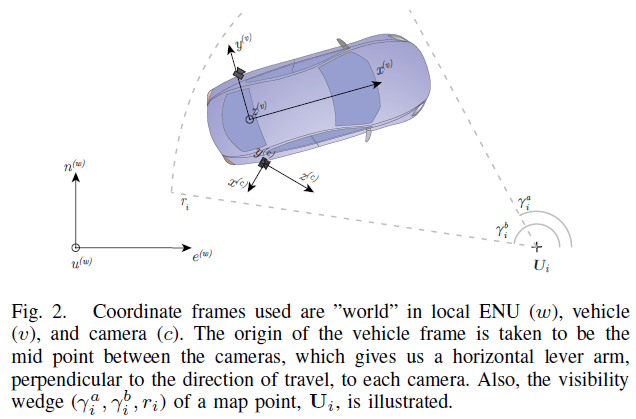
相机采集到的图片经过预处理,得到一组包含 $n_t$ 个特征点(坐标)与描述子对(即观测量),$\mathbf{f}_t=\{(u_t^i,d_t^i)\}_{i=1}^{n_t}$ ,在本文中,依据我们使用的方法不同,$\mathbf{f}_t$ 会有不同的形式:如果使用语义点云地图方法,$\mathbf{f}_t$ 是稠密的,包含图片中每一个像素,且描述子为像素对应的语义标签;若使用SIFT 算法,则特征点是稀疏的,且描述子为128x1 的向量。
2.2 Maps
假设预构建的特征地图包含M 个特征点,则地图可表示为 $\mathcal{M} = \{<\mathbf{U}_i, \mathbf{D}_i, \mathcal{V}_i>\}_{i=1}^M$ ,每个特征点包含位置信息 $\mathbf{U}_i$ ,特征描述子 $\mathbf{D}_i$ ,以及可视参数 $\mathcal{V}_i = [\rho_i, \gamma_i^a,\gamma_i^b,r_i]^T$ (参考Fig. 2),其中 $\rho_i$ 表示特征被探测到的概率。
2.3 Problem Definition
问题被描述为:给定观测和地图 $\mathcal{M}$ ,通过迭代计算出汽车相对于地图的位姿后验概率估计。
假设 $t$ 时刻的汽车位姿为 $\mathbf{x}_t$ ,则我们的目标为计算 $p(\mathcal{x}_t|\mathcal{f}_{1:t}, \mathcal{M})$ 。
3 Models
3.1 Process model
状态方程
作者使用一个简单的点质量模型 point mass model 来对汽车进行建模。本状态方程由两部分组成,部分一使用速度测量作为输入来对运动进行建模:
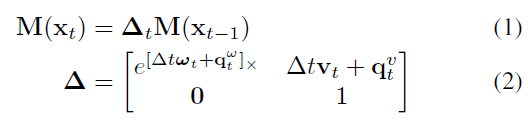
其中,$M(.) \in SE(3)$ ,是表示位姿的4x4 矩阵。
部分二是一项来确保总有一小部分density 被留在路上,这保证了即便一个lost filter 丢失了,也可以重新获取其横向位置。
综合以上两部分,状态模型表示为:
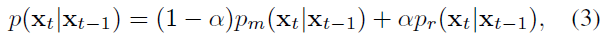
其中,$p_m(.)$ 是由部分一给定的,$p_r(.)$ 是 $p_m(.)$ 到路上的投影。
3.2 Measurement model
假定数据关联步骤已经解决,得到一个DA 向量 $\mathbf{\lambda}_t = [\lambda_t^1, …, \lambda_t^{n_t}]^T$ ,其中,$\lambda_t^i = j$ 表示,如果 $j>0$ ,则图片特征 i 与地图特征 j 相关联;否则该特征在地图中不存在。
利用已有的DA,并假定特征位置坐标和描述子 $u_t^i,d_t^i$ 满足条件独立,则有:
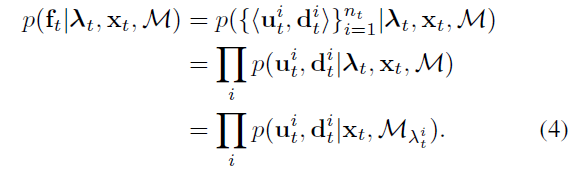
其中,$\mathcal{M}_{\lambda_t^i}$ 表示地图中带有描述子和可见参数的3D 点与图片中的特征点 i 根据DA $\mathbf{\lambda}_t$ 关联起来。
3.2.1 SIFT map
当给定数据关联时,特征中的描述子对似然函数没有帮助,可以忽略掉。同时,假定图片中SIFT 特征点的探测误差服从零均值高斯分布,则有:
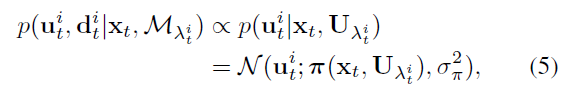
其中,$\pi(.)$ 表示带有镜头畸变的标准针孔相机投影模型;$\sigma_{\pi}^2$ 表示探测器误差的方差。
3.2.2 Semantic map
在该方法中,地图中的特征点描述子 $D_j$ ,以及图片特征的描述子 $d_t^i$ 都是来自CityScapes 数据集中的语义标签。
即便图片中相邻像素的语义分割结果是相关的,但是作者让做出了简化假设:假设像素坐标与语义类别是独立的,则有:
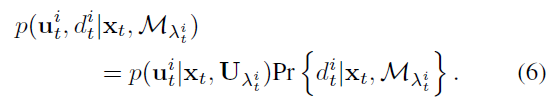
这个因式分解会在观测中导致overconfidence,而且观测越多影响越严重,这使得作者在第四章中加入了尺度参数 s,以及测量截断值 $N_c$ 。
上式的第一个因子 $p(u_t^i|x_t, U_{\lambda_t^i})$ 表示在像素 i 处检测到特征的概率,然而本方法是对整幅图片进行语义分割,即每一个像素都被视为一个特征,则该因子对于任意的 i 是一个常数值。因此,上式可进一步化简为:
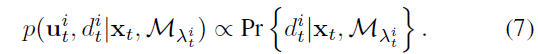
对于上式的右半部分,分两种情况讨论:
情况一:没有地图点投影到该像素,即 $\lambda_t^i = 0$ :此时,我们无法从地图中获取该像素类别的信息,作者为所有这种像素(没有地图特征点投影的像素)假设一种分布,即在所有种类上的边缘分布:
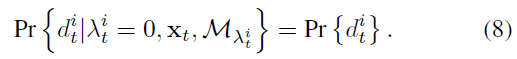
根据后文描述,该边缘分布是通过汇总制图所用到的所有图片的语义分割结果,统计各个种类所占的比例即为该边缘分布。
情况二:有地图点投影到该像素,即 $\lambda_t^i > 0$ :虽然地图上的一个特征点投影到了该像素上,但是仍然不能确定是探测到了这个地图特征点,还是该处被别的物体遮挡住了,如汽车或行人。为解决该不确定度,作者引入了一个探测变量 $\delta$ :当该值为1时表示该地图特征点确实被探测到了,否则为0。利用该探测变量,将像素与对应的地图特征点似然函数表示为:
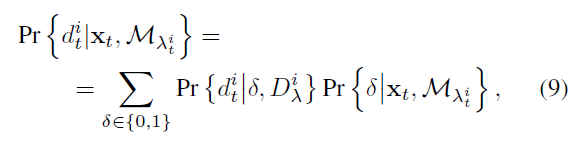
其中,$Pr\{d_t^i|\delta=0, D_{\lambda^i_k}\}, Pr\{d_t^i|\delta=1, D_{\lambda^i_k}\}$ 分别表示给定特定地图点特征被遮挡或者可视状态下像素类别的概率;根据后文描述, $Pr\{d_t^i|\delta=0, D_{\lambda^i_k}\}$ 是通过手动调整设定的,动态物体的概率设定高一点,如汽车、行人等,静态物体设置低一点; $Pr\{d_t^i|\delta=1, D_{\lambda^i_k}\}$ 的确定是通过汇总确定该地图特征点的所有图片中,该点周围7x7 邻域像素的语义分类,并归一化为一个直方图作为各个种类的PMF;剩下的部分表示给定的地图点是可视的概率:
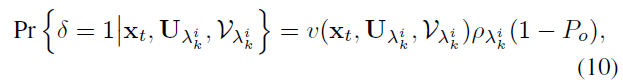
其中,$v(.)$ 是一个函数,当位姿 $\mathbf{x}_t$ 在地图特征点的可视区域内时该函数为1;$P_0$ 表示一个可视地图特征点被遮挡的概率。
综上所述,语义地图法的似然计算需要考虑地图特征点是否映射到像素上的两种情况:
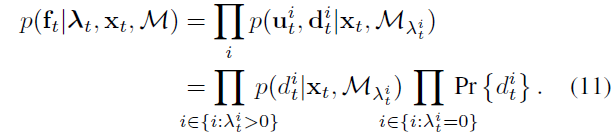
4 Algorithmic Details
4.1 SIFT filter
针对该方法,作者使用了无迹卡尔曼滤波器UKF 进行优化,伪代码如下所示:

其中,数据关联DA 步骤如下所示:作者基于当前的位姿估计以及地图特征点的可视参数 $\mathcal{V}$ 来选取一个子地图 $\mathcal{M}_t$ ,将图片中提取到的SIFT 特征点与子地图 $\mathcal{M}_t$ 中的特征点进行匹配,并使用RANSAC 算法进行外点剔除,最终得到DA 。
4.2 Semantic filter
针对该方法,作者使用了bootstrap particle filter 进行递归优化,该算法的伪代码如下所示:

为了可以评估一个粒子的似然,需要确认地图中的哪些特征点是潜在可视的,这与SIFT 方法类似,但是只需要做到近似即可,因此可以同时计算附近的几个粒子,例如使用这些粒子的平均位置和地图特征点的可视参数进行计算。然后,将这些潜在可视的地图特征点映射到图片中,从而为每个粒子构建了独有的数据关联 $\lambda_t$ 。

将式(11)除以常数 $\prod_iPr\{d_t^i\}$ 可以简化权重更新过程,因为只需要考虑那些有地图特征点投影到的像素,
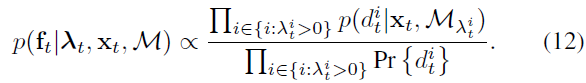
在3.2.2节我们做了像素位置与语义分类条件独立的假设,但实际情况是该假设不满足,所以会导致对观测的overly confident,为减小该假设的影响,作者增加测量似然到一个小于1的正数,因此,对于粒子 j 的权重更新变为了:
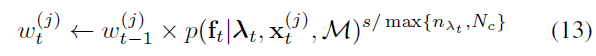
其中,$w_t^{(j)}$ 是在状态 $\mathbf{x}_t^{(j)}$ 下粒子 j 的权重;s 是尺度参数,本文设定为3;$n_{\lambda_t}$ 是映射到图像中的地图特征点个数;$N_c = 400$ 是截断值,作者认为更多的映射特征点不会提供更多的信息,因为更多的特征点意味着它们之间的间距越小,那么它们之间的相关性越强。