Nicholson, Lachlan, Michael Milford, and Niko Sunderhauf. “QuadricSLAM: Dual Quadrics From Object Detections as Landmarks in Object-Oriented SLAM.” IEEE Robotics and Automation Letters 4, no. 1 (January 2019): 1–8. https://doi.org/10.1109/LRA.2018.2866205.
1 Introduction
作者认为语义地图应该是面向对象的 object-oriented,即将对象视为地图的中心实体,而二次曲面(如椭球体 ellipsoids)有着很多具有吸引力的特性来作为面向对象语义地图的地标表示方法,如Fig. 1 所示,二次曲面可以紧凑表示,且可在投影集合框架中实现高效操纵;二次曲面可以表示物体的尺寸、位置及朝向信息,而且如果必要的话,可以作为更详细3D 重建的anchors。此外,二次曲面表示形式在整合角度来看也具有吸引力,作者会在后文中证明,二次曲面可以直接利用物体检测bbox 进行构建,而且很方便整合进基于因子图的SLAM 框架中。

本文做出的贡献:
- 将SLAM 中的物体地标使用受限二次曲面 constrained dual quadrics 进行参数化表示;
- 作者将物体检测网络(如YOLOv3)视为SLAM系统中的传感器,将其观测(物体 bbox)通过几何误差方程来直接约束二次曲面参数;
- 为了将二次曲面参数表示整合进SLAM 系统中,作者构建了一个基于因子图的SLAM 方程,可联合估计二次曲面和载体位姿参数(在假设解决了物体关联前提下 assuming solved data association)。
3 Dual Quadrics——Fundamental Concepts
3.1 Dual Quadrics
二次曲面是3D 空间中的曲面,可使用4x4 对称矩阵 $Q$ 来表示;in dual form,一个二次曲面可以使用一组正切平面来定义,这些平面组成一个二次曲面的包络envelope,因此,对偶二次曲面dual quadric $Q^\ast$ 定义为满足 $\pi^TQ^\ast\pi = 0$ 的所有平面 $\pi$ 。二次曲面包含的立方体包括球体、椭球体、双曲面、圆锥体和圆柱体。
二次曲面包含9自由度,对应于4x4 对称矩阵 $Q$ 中10个独立的元素,多余的一个元素表示尺寸信息。因此,可以使用10维向量来表示一个对偶二次曲面:$\hat{\mathbf{q}} = (\hat{q}_1, …, \hat{q}_{10})$ ,其中的每个元素对应于 $Q^\ast$ 的10个独立元素。
对偶二次曲面投影至图像平面上为一个对偶二次曲线:$\mathbf{C}^\ast = \mathbf{P}\mathbf{Q}^\ast\mathbf{P}^T$ ,其中 $\mathbf{P} = \mathbf{K}[\mathbf{R} | \mathbf{t}]$ 为相机投影矩阵,包含内参和外参。二次曲面包含的曲线包括圆、椭圆、抛物线和双曲线。
3.2 Constrained Dual Quadric Parameterization
由于二次曲面可以是闭合曲面也可以是非闭合曲面(如抛物面和双曲面),只有闭合曲面才可以表示有意义的物体地标,所以作者使用受限对偶二次曲面表示形式来确保曲面是闭合的椭球体或球体。作者将对偶二次曲面表示为:

其中,$\overset{\frown}{\mathbf{Q}}^\ast$ 为一个中心位于原点的椭球体,$\mathbf{Z}$ 表示齐次变换矩阵,包含旋转和平移:
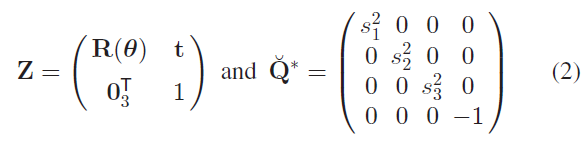
其中,$\mathbf{t} = (t_1, t_2, t_3)$ 为平移向量;$\mathbf{R}(\mathbf{\theta})$ 为由角度 $\mathbf{\theta} = (\theta_1, \theta_2, \theta_3)$ 定义的旋转矩阵;$\mathbf{s} = (s_1, s_2, s_3)$ 为椭球体三个轴的尺度参数。在后续中,作者使用9维向量表示一个受限对偶二次曲面:$\mathbf{q} = (\theta_1, \theta_2, \theta_3, t_1, t_2, t_3, s_1, s_2, s_3)$ ,并根据式1来重建完整的对偶二次曲面 $\mathbf{Q}^\ast$ 。
4 A Sensor Model for Image-Based Object Detections
4.1 Motivation
作者的目标是将SOTA 物体检测器作为一个传感器整合进SLAM中,因此,需要构建一个传感器模型,在给定预估相机位姿 $\mathbf{x}_i$ 和预估地图结构(如二次曲面参数 $\mathbf{q}_j$ )时可以预测物体检测器的观测参数。物体检测器的观测包含物体检测bbox 和对应的物体标签,本文主要关注bbox 参数,作者使用 $\mathbf{b} = (x_{min}, y_{min}, x_{max}, y_{max})$ 来表示bbox ,因此,该传感器模型可表示为:$\beta(\mathbf{x}_i, \mathbf{q}_j) = \hat{\mathbf{b}}_{ij}$ ,即根据相机位姿 $\mathbf{x}_i$ 和二次曲面参数 $\mathbf{q}_j$ 来预测bbox 观测 $\hat{\mathbf{b}}_{ij}$ 。
在构建了该传感器模型后,作者可以在预测和观测之间形成几何误差项,这对于本文提出的SLAM 系统至关重要。
4.2 Deriving the Object Detection Sensor Model $\beta$
将二次曲面 $\mathbf{q}_j$ 根据相机位姿 $\mathbf{x}_i$ 投影至图像中:$\mathbf{C}^\ast_{ij} = \mathbf{P}_i\mathbf{Q}^\ast_{(q_j)}\mathbf{P}^T_i$ ,其中 $\mathbf{P} = \mathbf{K}[\mathbf{R} | \mathbf{t}]$ 为相机投影矩阵,包含相机内参 $\mathbf{K}$ 和相机位姿;由此获得对偶双曲线 $\mathbf{C}^\ast$ ,并进一步获取其原始形式 $\mathbf{C}$ 。简单的模型会直接计算二次曲线 $\mathbf{C}$ 的闭合bbox,并将该bbox 截断来适应图片边界,如Fig. 2(a)所示,当该二次曲线大部分位于图像边界外时,二次曲线 $\mathbf{C}$ 在图片内对应的bbox(蓝色虚线)与真值bbox (绿实线)之间存在较大的差异,即该方法会引入极大的误差。
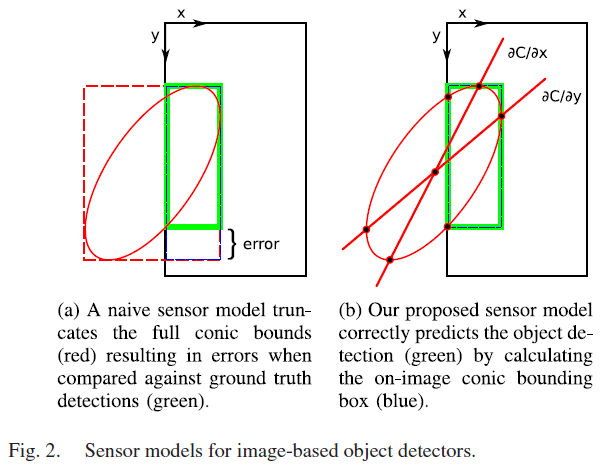
一个准确的传感器模型需要获取二次曲线和图片边界的交点,对于物体检测bbox 的正确预测应该是最小轴对齐的矩形,该矩形在将图片尺寸内的二次曲线完全包括进去,该矩形bbox 表示为:
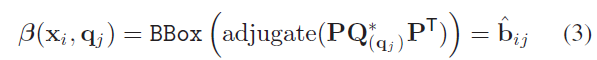
4.3 Calculating the On-Image Conic Bounding Box
通过以下算法来获取图片中双曲线的正确bbox:
- 寻找该二次曲线上包含极值坐标的四个点 $\{\mathbf{p}_1, …, \mathbf{p}_4\}$ ;
- 寻找该二次曲线与图片边界的交点(最多8个) $\{\mathbf{p}_5, …, \mathbf{p}_{12}\}$ ;
- 移除 $\mathcal{P} = \{\mathbf{p}_1, …, \mathbf{p}_4\}$ 中所有的non-real 点和位于图片边界外的点;
- 从 $\mathcal{P}$ 中的剩余点获取极值坐标点。
经过以上步骤,可以得到向量:
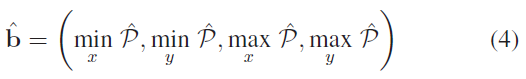
上式表示的bbox 即可完整包含二次曲线 $\mathbf{C}$ 在图片可见区域的部分。
5 SLAM With Dual Quadric Landmark Representations
5.1 General Problem Setup
作者构建如下的SLAM 问题方程:$\mathbf{x}_{i+1} = f(\mathbf{x}_i, \mathbf{u}_i) + \mathbf{w}_i$ ,其中,$\mathbf{u}_i$ 表示连续两个位姿 $\mathbf{x}_i, \mathbf{x}_{i+1}$ 之间的里程计观测;$f$ 通常为非线性方程;$\mathbf{w}_i$ 为零均值高斯分布,协方差为 $\sum_i$ 。此处不具体讨论里程计观测 $\mathbf{u}_i$ 的具体获取形式。
此外,还有物体路标观测 $B = \{\mathbf{b}_{ij}\}$ ,表示在位姿 $\mathbf{x}_i$ 处对物体 $j$ 观测到的bbox 。
值得注意的是,作者在此假设数据关联问题已经得到解决。
5.2 Building and Solving a Factor Graph Representation
条件概率分布可表示为因子式:
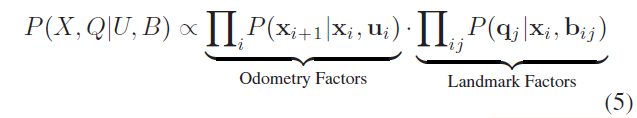
包含:载体位姿 $X = \{\mathbf{x}_i\}$ ,地标 $Q= \{\mathbf{q}_i\}$ ,里程计观测 $U= \{\mathbf{u}_i\}$,物体观测 $B= \{\mathbf{b}_{ij}\}$。
里程计因子 $P(\mathbf{x}_{i+1} | \mathbf{x}_i, \mathbf{u}_i)$ 假设服从高斯分布,即 $\mathbf{x}_{i+1} \sim \mathcal{N}(f(\mathbf{x}_i, \mathbf{u}_i), \sum_i)$ 。为了将地标因子集成至高斯因子图中,应用贝叶斯法则:
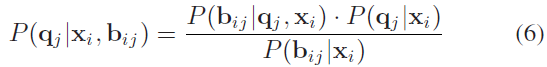
因为目标是求取MAP,所以忽略分母项(只发挥归一化作用)。进一步地,作者假设 $P(\mathbf{q}_{j} | \mathbf{x}_i)$ 服从均匀分布,则式6可转化为求取最大似然 $P(\mathbf{b}_{ij} | \mathbf{q}_j, \mathbf{x}_i)$ 。该似然项可建模为高斯分布 $\mathcal{N}(\beta_{(\mathbf{x}_i, \mathbf{q}_j)}, \Lambda_{ij})$ ,其中,$\beta$ 为上节构建的传感器观测模型,$\Lambda$ 为协方差矩阵,表示观测到的检测物体在图片空间中的不确定性。
式5的解可视为求解非线性最小二乘问题:

其中,第一项的差值是SE(3) 空间的差值。
5.3 The Geometric Error Term
式7的第二项 $||\mathbf{b}_{ij} - \beta_{(\mathbf{x}_{i}, \mathbf{q}_{j})}||^2_{\Lambda_{ij}}$ 是一个几何误差项,因为 $\mathbf{b}, \beta$ 都是包含像素坐标的向量,作者发现该几何误差项要比之前工作中的代数误差项更具优势。且,可以通过协方差矩阵项 $\Lambda_{ij}$ 更方便地将物体检测器的空间不确定性传递至SLAM 系统中。
5.4 Variable Initialization
载体位姿 $\mathbf{x}_i$ 可通过里程计观测值 $\mathbf{u}_i$ 进行初始化,接下来讨论对偶二次曲面地标 $\mathbf{q}_j$ 的初始化。可通过最小二乘满足以下定义式来进行初始化:

其中,$\hat{\mathbf{q}_j}$ 为3.1节的通用对偶二次曲面:$\hat{\mathbf{q}} = (\hat{q}_1, …, \hat{q}_{10})$ 。
可使用地标bbox 观测 $\mathbf{b}_{ij}$ 和对应的线 $\mathbf{l}_{ijk}$ (bbox的4条线)来定义平面 $\mathbf{\pi}_{ijk}$ : $\mathbf{\pi}_{ijk} = \mathbf{P}^T_i \mathbf{l}_{ijk}$,其中,相机位姿 $\mathbf{P}_i$ 可通过初始位姿估计获取,最终,式8可转换为:
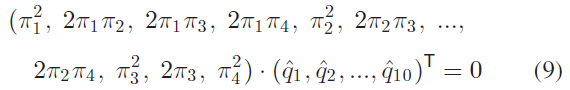
使用不同视角 $i$ 和平面 $k$ ,基于式9构建线性方程组,通过SVD 分解获取最小二乘解 $\hat{\mathbf{q}}_j$ 。该解是一个通用的二次曲面,并没有被约束为一个椭球体,这里会进一步使用3.2节的方式将其进一步参数化表示,参数求取过程如下所述:
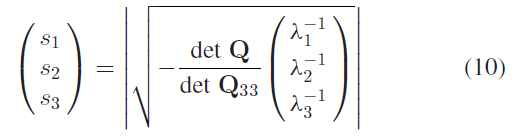
其中,$\mathbf{Q}_{33}$ 为二次曲面矩阵 $\mathbf{Q}$ 的左上侧3x3 子矩阵;$\lambda_i$ 为 $\mathbf{Q}$ 的特征值;旋转矩阵 $\mathbf{R}(\theta)$ 为 $\mathbf{Q}_{33}$ 的特征矩阵;平移向量表示为 $\mathbf{t} = (\hat{q}_4, \hat{q}_7, \hat{q}_9)/\hat{q}_{10}$ 。
6 Experiments and Evaluation
作者在TUM 数据集上进行测试,与两种里程计算法进行比较,分别是Fovis 和 ORB-SLAM2 算法,物体检测器使用YOLOv3网络;里程计噪声模型中的平移和旋转标准差均设置为0.001,物体bbox 的标准差是计算该物体所有观测bbox 长与宽的标准差之和。定位误差ATE 如Table 1所示,
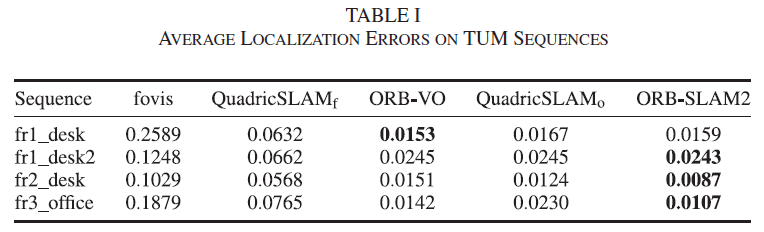
可以发现,相较于fovis 视觉里程计,加入二次曲面物体地标后定位精度提升明显,但较ORB-SLAM2 有所下降,作者认为原因可能有两个:
- bbox 观测噪声不太符合高斯分布;
- 物体遮挡导致过小的bbox观测,从而影响定位精度。
作者通过进一步实验:对于fr1_desk2, fr3_office 数据序列,作者舍弃宽高标准差大于一定值的物体bbox ,从而实现两个数据序列的定位精度分别达到0.0239和0.0087。