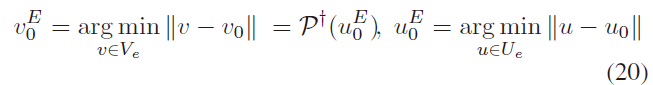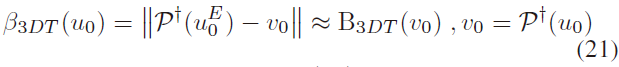Liao, Ziwei, Yutong Hu, Jiadong Zhang, Xianyu Qi, Xiaoyu Zhang, and Wei Wang. “SO-SLAM: Semantic Object SLAM With Scale Proportional and Symmetrical Texture Constraints.” IEEE Robotics and Automation Letters 7, no. 2 (April 2022): 4008–15. https://doi.org/10.1109/LRA.2022.3148465.
1 Introduction
本文主要解决单目 Object SLAM 的两个挑战:
- 单目相机包含较少的物体约束信息,特别是在部分观测、遮挡等情况下更为严重,使得单目 Object SLAM 较为脆弱;
- 当前的 Object SLAM 主要用于约束物体的占用空间,没有充分利用物体的朝向信息。
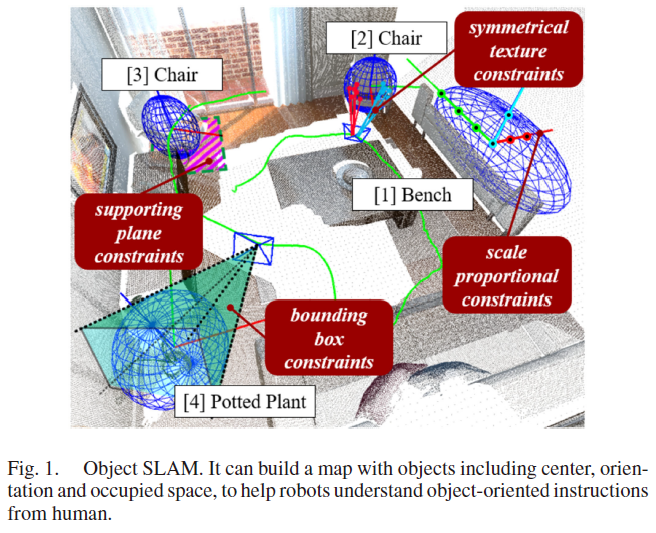
针对以上两个挑战,作者提出了单目 Semantic Object SLAM (SO-SLAM) 系统,如Fig. 1 所示,除了物体的语义信息,作者还引入了三种代表性的物体空间约束:尺寸比例约束、对称纹理约束以及平面支撑约束,作者推导约束模型并同时应用于前端初始化与后端优化中。
本文的贡献如下:
- 提出一个面向室内环境的完全耦合三种空间约束的单目 Object SLAM;
- 基于空间约束提出两个新方法:单帧物体初始化方法和物体朝向优化方法;
- 在两个公开数据集与自采数据集上验证了本算法的有效性。
3 Monocular Object SLAM Framework
表示物体的椭球体包含9自由度,可利用SVD 方法来获取,该方法至少3帧具有足够视差的观测才可以获取(Nicholson 等, 2019)。作者利用位姿图对相机和物体位姿进行优化:
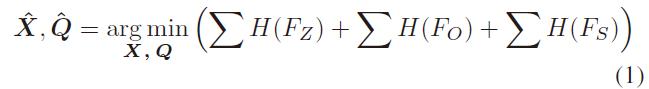
其中,X 表示相机位姿,Q 表示物体位姿;$F_Z$ 表示相机-物体观测约束,$F_O$ 表示里程计约束,这两个约束项在文章(Nicholson 等, 2019)中有详细介绍;本文着重介绍新增加的空间约束 $F_S$ ,包含平面支撑约束 $f_{sup}$ ,尺度比例约束 $f_{ssc}$ ,以及对称纹理约束 $f_{sym}$ ;H() 是鲁棒核用以提高系统对外点的鲁棒性,本文使用 Huber Kernel。
4 Single-Frame Initialization with Semantic Priors
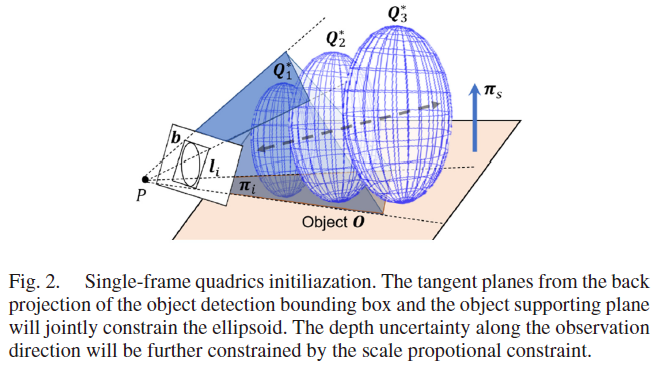
作者根据人类认知习惯来设定物体坐标系:人造物体的上表面一般与物体的支撑面相反,前向一般是对称的方向,由此构建物体的 Z 轴和 X 轴,由此构建了物体坐标系。然后,就可以应用更多的约束,如Fig. 2所示,实现单帧图片对9自由度物体进行初始化的方法,克服了传统SVD 方法难以满足的要求。
4.1 Object Detection Constraints
物体检测框的四条边线经相机投影矩阵进行逆投影,可得到四个切面约束,如Fig. 2中的对 $l_i$ 逆投影得到切平面 $\pi_i$ ,由此形成对椭球体 $Q^*$ 的四自由度约束,如下所示:
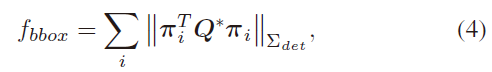
其中,$\sum_{det}$ 表示物体检测协方差矩阵,本文中令其为10。
4.2 Plane Supporting Constraints
根据物体与其支撑平面的关系,可以构建三个约束,如Fig. 2所示,物体的X、Y轴与平面 $\pi_s$ 的法向量正交,椭球体与平面 $\pi_s$ 相切。由此构建如下函数模型:
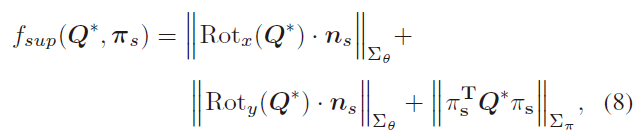
其中,$Rot_x(Q^\ast), Rot_y(Q^\ast)$ 分别为椭球体的 X、Y 轴;支撑平面为 $\pi_s=(n_s, d)$, $n_s$ 为支撑平面的法向量。
4.3 Semantic Scale Proportional Constraint
作者提出了一种灵活的物体尺度先验约束——Scale Proportional Constraint (SPC),用来约束物体的尺寸比例而不是其精确的尺寸。假设物体的尺寸为 $s = [a, b, c]^T$ ,分别为X、Y、Z轴的尺寸,作者由此定义尺寸比例 $r = [\sigma, \beta]^T$ :

根据常见的物体尺寸可制作一个尺寸比例表。
给定一个物体 $Q_O^\ast$ ,可根据定义计算其尺寸比例 $r_O = r(Q^\ast_O)$ ,根据其语义类别标签 $l_O$ 经查表可得其对应的尺寸比例 $r_s = SemTable(l_O)$ 。由此构建物体的尺寸比例约束:
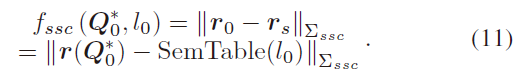
4.4 Solving the Single Frame Initialization
利用Levenberg-Marquardt 算法对目标方程进行迭代求解:
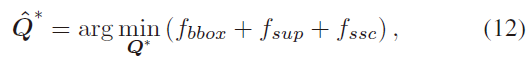
5 Orientation Optimization with Texture Symmetry
5.1 Mathematical Description of Object Symmetry
人造物体一般是对称的,作者将其对称平面的方向定义为前向,也就是物体坐标系的 X 轴,如Fig. 3所示。物体对称性可数学表示为:物体上的任意一点 $v_0 \in V$ 都可经由其对称面 $\pi_{xz}$ 找到物体上与其对称的点 $v_0^S \in V$ 。
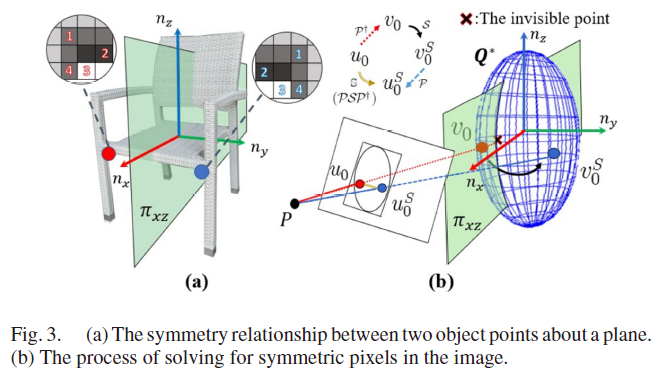
物体在图像中的一点 u 经逆投影得到其在3D 空间中的点 v,满足以下方程:
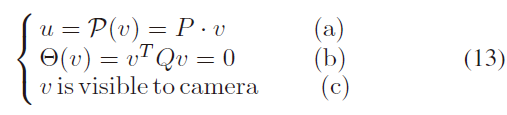
将式(a)代入式(b),在(c)的约束下最多只有一个解,由此可以得到 u 的对称像素点:
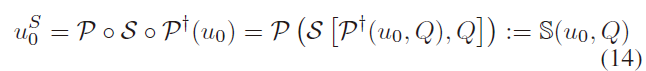
其中,$\mathcal{P}$ 表示相机的投影矩阵;$v_0^S = \mathcal{S}(v_0, Q)$ 表示3D 点 $v_0$ 的对称点。该过程如Fig. 3(b)所示,根据找到的对称点对,作者构建一个描述子映射关系 $\beta()$ ,作者称其为*对称投影不变 symmetric projection invariant,其满足以下性质:
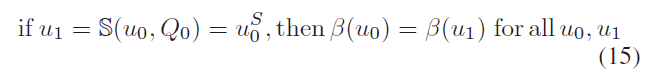
由此,当观测噪声较严重时,可以构建如下的代价方程来优化椭球体 Q:
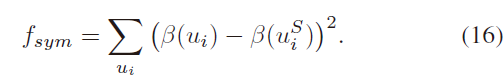
5.2 The Construction of Symmetry Descriptor
对于 $\beta(*)$ 的确定,作者先后考虑了灰度值(广泛用于直接法)、BRIEF 描述子等,之后,作者考虑像素的 Distance Transform:
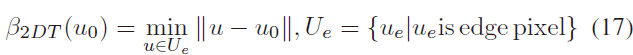
上式的含义为:从一个像素点到图像中任意边上像素的最近距离,部分反应了物体的纹理。但是这个描述子不一定可以满足对称投影不变的性质,如Fig. 4(a)所示。进而,作者发现了the nearest edge distance of point $v_0$ ,记为 $B_{3DT}(v_0)$ 可满足要求(但计算量太大):
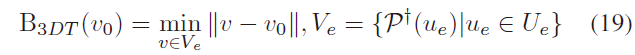
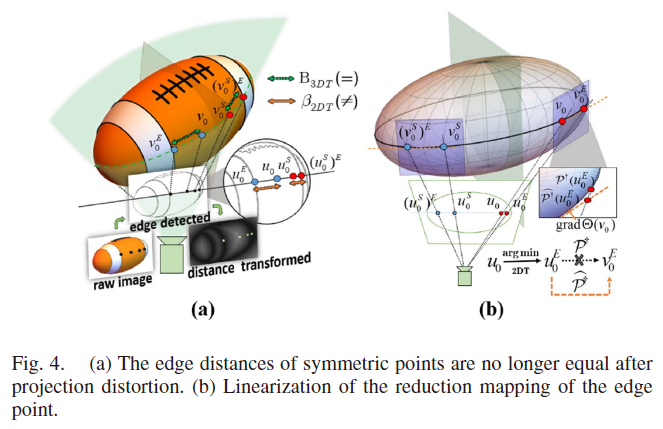
作者结合以上两种方法的优势,提出了 Improved-DT descriptor: