Bowman, Sean L., Nikolay Atanasov, Kostas Daniilidis, and George J. Pappas. “Probabilistic Data Association for Semantic SLAM.” In 2017 IEEE International Conference on Robotics and Automation (ICRA), 1722–29. Singapore, Singapore: IEEE, 2017. https://doi.org/10.1109/ICRA.2017.7989203.
1 Introduction
本文做出的贡献:
- 第一个将惯性、几何以及语义观测信息紧耦合至一个优化框架的定位算法;
- 将联合metric-semantic SLAM 问题分解为连续(位姿)和离散(数据关联DA和语义标签)优化子问题;
- 在包含光照变化的杂乱场景中利用里程计和视觉测量信息进行室内外真实场景的长轨迹测试实验。
2 Probabilistic Data Association in SLAM
经典的SLAM问题可表述如下:移动传感器穿越一个未知环境,环境中包含M 个静态路标集合 $\mathcal{L} = \{l_m\}^M_{m=1}$ ,给定一组传感器测量数据 $\mathcal{Z} = \{z_k\}^K_{k=1}$ ,任务是估计地标位置 $\mathcal{L}$ 以及传感器的位姿序列 $\mathcal{X} = \{x_t\}^T_{t=1}$ 。
大部分现有的工作都聚焦于估计 $\mathcal{L}$ 和 $\mathcal{X}$ ,很少强调数据关联 $\mathcal{D}$ 实际上是未知的。这里的数据关联 $\mathcal{D} = \{(\alpha_k, \beta_k)\}^K_{k=1}$ 指的是在传感器位姿 $x_{\alpha_k}$ 情况下对路标 $l_{\beta_k}$ 的观测数据为 $z_k$ ,即在相机位姿 $x_{\alpha_k}$ 下,观测数据 $z_k$ 和路标 $l_{\beta_k}$ 之间的关联。
SLAM问题的求解可表述为:在给定观测数据 $\mathcal{Z}$ 时,求解 $\mathcal{L}$ ,$\mathcal{X}$ 和 $\mathcal{D}$ 的最大似然估计:
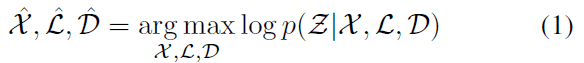
求解方法一:
给定先验估计 $\mathcal{X}^0,\mathcal{L}^0$ ,求得数据关联的最大似然估计 $\hat{\mathcal{D}}$ ,然后利用 $\hat{\mathcal{D}}$ 计算路标与传感器状态 $\mathcal{L}$ ,$\mathcal{X}$ 的最大似然估计。
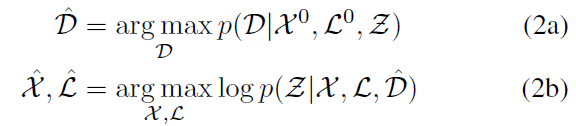
上述方法的缺点在于,错误的数据匹配会严重影响估计结果;而如果为了避免错误匹配而舍弃模糊测量,在后续位姿优化后也无法利用这些模糊测量。
求解方法二:坐标下降法coordinate descent
为了避免方法一简单的一步处理,本方法使用迭代计算:
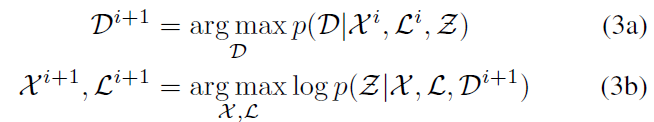
本方法可以在状态估计得到优化后返回来重新估计数据关联;然而,本方法不能解决模糊测量的问题,因为仍然需要一个硬数据关联。
为解决模糊测量导致的数据关联问题,当估计数据关联时,作者不是简单地选取物体属于某个特定的类别 $\hat{\mathcal{D}}=p(\mathcal{D}|\mathcal{X}, \mathcal{L}, \mathcal{Z})$ ,而是考虑观测数据与路标之间所有可能的数据关联 $D$ 。给定一个初始估计 $\mathcal{X}^i, \mathcal{L}^i$ ,使用 $\mathcal{D}$ 中的全部可能可得到一个更优的估计值,作者采用了expectation maximization (EM) 方法来最大化 expected measurement likelihood 进行计算:
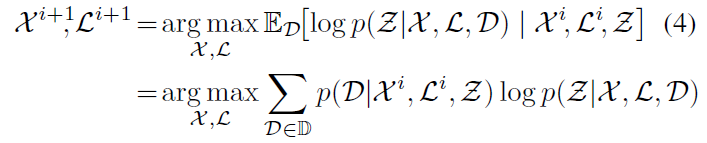
其中, $\mathbb{D}$ 是 $\mathcal{D}$ 的所有取值空间。本EM 方程优势在于不需要硬数据关联 hard decisions on data association,而是平均所有可能的数据关联情况。
为了与坐标下降法进行比较,上式可重写为:
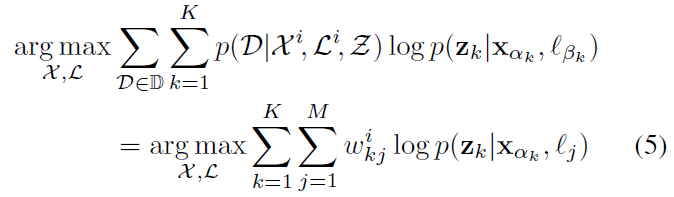
其中,$w_{kj}^i$ 是一个量化了软数据关联的权重参数,表示K 个观测和M 个路标之间所有关联对应的权重参数,$w_{kj}^i = \sum_{\mathcal{D}\in\mathbb{D}(k,j)}p(\mathcal{D}|\mathcal{X}^i, \mathcal{L}^i, \mathcal{Z})$ ,其中,$\mathbb{D}(k,j) = \{\mathcal{D}\in\mathbb{D} | \beta_k = j\}\subseteq \mathbb{D}$ 是观测 $k$ 分配给地标 $j$ 的所有数据关联组合。
上式的求解同样采用EM 方法:
- E 步骤:以权重参数 $w_{kj}^i$ 的形式来估计数据关联分布 $p(\mathcal{D}|\mathcal{X}^i, \mathcal{L}^i, \mathcal{Z})$ ;
- M 步骤:根据E 步骤计算得到的分布来最大化 expected measurement log likelihood。
3 Semantic SLAM
作者设定地标的状态 $l$ 包含位置信息 $l^p \in \mathbb{R}^3$ 和类别标签 $l^c$ 。为了估计地标状态 $\mathcal{L}$ (位姿与种类)和传感器运动轨迹 $\mathcal{X}$ ,作者使用三种信息源:惯性、几何点特征和物体语义观测。

3.1 Inertial information
作者每隔n 帧选取一张单目相机采集到的图像作为关键帧,第t 帧对应的传感器状态表示为 $x_t$ ,包含6自由度的位姿、速度以及IMU 偏差值。在相邻两个关键帧之间还有一组IMU 测量数据 $\mathcal{I}$ ,包含线性加速度和旋转角速度。
3.2 Geometric information
作者从每一个关键帧中提取ORB 特征点,并与后续的关键帧进行匹配。
3.3 Semantic information
从第t 个关键帧中检测到一组物体 $\mathcal{S}_t$ ,其中每个物体表示为 $\mathbf{s}_k = (s_k^c, s_k^s, s_k^b) \in \mathcal{S}_t$ ,三个参数分别表示所属的物体种类、量化的检测置信度得分,以及bounding box。本文的物体检测使用deformable parts model (DPM) 算法完成,该算法可以在CPU上实时运行。
如果语义观测 $\mathbf{s}_k$ 的数据关联 $\mathcal{D} = \{(\alpha_k, \beta_k)\}$ 已知,语义观测似然可以分解为:
其中,类别估计概率分布 $p(s_k^c|l_{\beta_k}^c)$ 对应于物体检测的混淆矩阵,其与得分分布(置信度)$p(s_k^s|l_{\beta_k}^c,s_k^c)$ 可以经过离线学习获取。而bounding-box 似然 $p(s_k^b|x_{\alpha_k},l_{\beta_k}^p)$ 被假设服从正态分布,其均值为物体中心在成像平面上的透视投影 (???),协方差与探测的bounding-box 尺寸成比例关系。
作者将语义SLAM 问题表述如下:
给定惯性测量 $\mathcal{I} = \{\mathcal{I}_t\}^T_{t=1}$ ,几何测量 $\mathcal{Y} = \{\mathcal{Y}_t\}^T_{t=1}$ 和语义测量 $\mathcal{S} = \{\mathcal{S}_t\}^T_{t=1}$ ,估计传感器的状态轨迹 $\mathcal{X}$ 以及环境中物体的位置和类别 $\mathcal{L}$ 。
作者使用惯性和视觉几何测量信息来跟踪传感器的局部运动轨迹,不恢复几何结构。而语义测量信息用来构建包含物体信息的地图用以回环检测,不仅鲁棒性更好、精确度更高,而且相较于保留全部几何结构信息的SLAM 方法更为高效。
4 Semantic SLAM using EM
在优化过程中,作者除了将数据关联视为一个隐变量外,也将离散的路标类别视为一个隐变量,从而对离散变量和连续变量完成干净且高效的区分。
几何特征点的数据关联由现有的特征跟踪算法提供,因此,本文提到的隐变量为语义观测信息的数据关联 $\mathcal{D}$ 和地标所属类别 $l_{1:M}^c$ 。
利用EM 求解语义SLAM 过程如下:
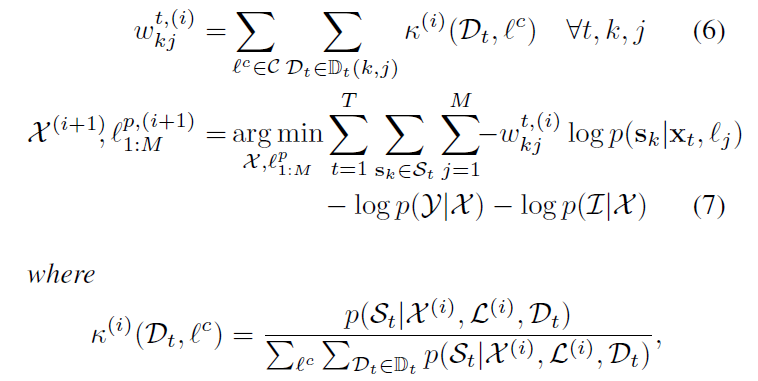
其中,$\mathbb{D}_t$ 是在时间戳 t 时刻观测数据中所有可能数据关联的组合,$\mathbb{D}_t(i,j)\subseteq \mathbb{D}_t$ 是所有可能的数据关联中观测 $i$ 分配给地标 $j$ 的组合。
Object classes and data association (E step)
一旦每一个测量-地标匹配对的权重参数 $w_{kj}^{t,(i)}$ 得到之后,即可用于传感器状态和地标位置的连续优化中。此外,物体类别的最大似然 $l^c$ 也可以通过计算得到的 k 值进行恢复:
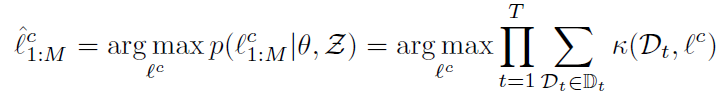
Pose graph optimization (M step)
作者使用位姿图进行优化。图包含一组顶点 $\mathcal{V}$ ,每个顶点对应一个优化变量;顶点之间还包含一组因子 $\mathcal{F}$ ,对应损失函数。优化方程如下所示:
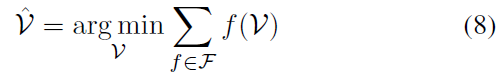
前人的工作使用硬数据关联 a hard data association,在传感器位姿节点和地标节点之间定义一个单独的因子factor;而本文考虑使用soft semantic data association multiple factors,在节点间使用多个因子进行关联:Semantic Factors, Geometric Factors and Inertial Factors。