Qin, Tong, Peiliang Li, and Shaojie Shen. “VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator.” IEEE Transactions on Robotics 34, no. 4 (August 2018): 1004–20. https://doi.org/10.1109/TRO.2018.2853729.
1 Introduction
集成IMU 观测可通过减少由于光照变化、纹理稀少区域或运动模糊造成的视觉跟踪精度损失,来大幅提高运动跟踪的表现。但是,单目VINS (Visual-Inertial System) 在使用中也有一些问题需要解决:
- 第一个问题是初始化困难:由于缺失直接的距离观测,很难直接将单目视觉结构与惯性测量进行融合;
- 其次是VINS 严重的非线性问题:这会在估计器初始化过程中带来巨大的挑战,再大部分场景中系统需要放置在一个位置已知的静态区域,然后缓慢小心地移动,这会极大限制系统的应用场景;
- 另一个问题是VIO 的长期漂移问题:为了消除累积漂移,会使用回环检测、重定位及全局优化技术;
- 此外还有对于地图保存与重使用的需求正在不断增长。
为解决上述问题,作者提出了VINS-Mono 系统——一个鲁棒且多功能的单目视觉-惯性状态估计器,该系统包含以下特点:
- 鲁棒的初始化程序使得系统可以在未知状态进行启动;
- 紧耦合、基于优化的单目VIO 带有相机-IMU 外参标定和IMU 偏差校正;
- 在线重定位以及4自由度的全局位姿图优化;
- 位姿图重用可保存、载入并融合多个局部位姿图。
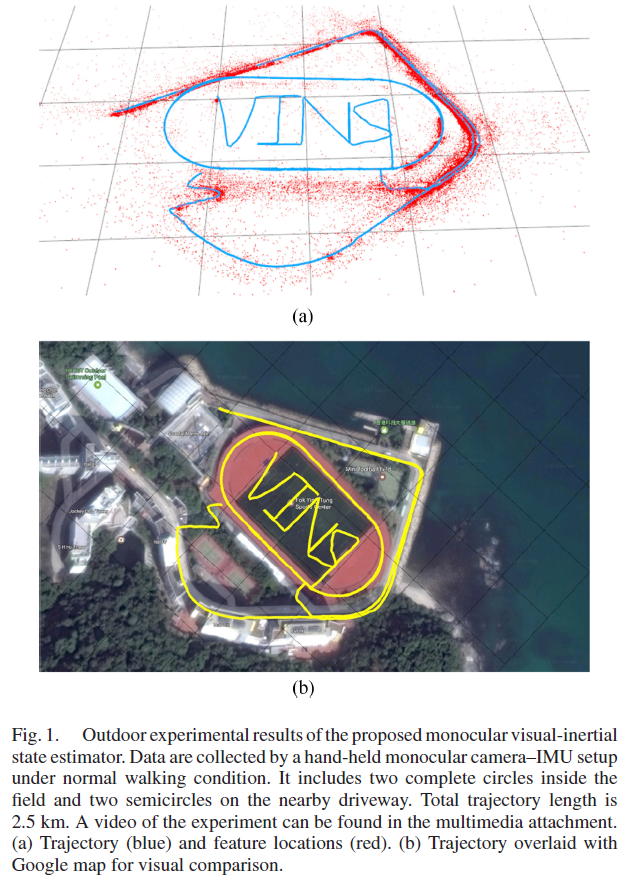
该系统已经成功应用于小规模的AR 场景、中规模的无人机导航,以及大规模的状态估计任务,如Fig. 1所示:
3 Overview
本文提出的单目视觉-惯性状态估计器的架构如Fig. 2所示,
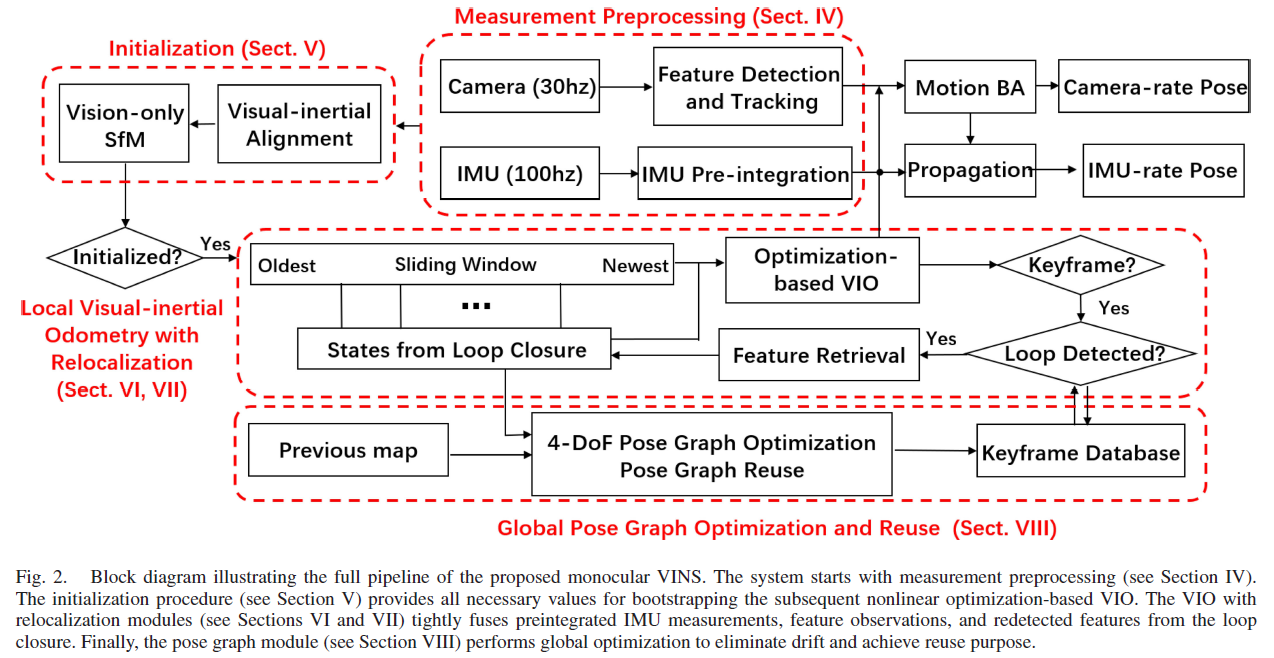
相较于适用于双目相机的SOTA 算法OKVIS,本算法是专为单目相机设计的,作者针对性设计了初始化程序、关键帧选取标准,并使用具有大视角的相机进行更好地跟踪;此外,本算法作为一个完整的系统还包含了回环检测以及位姿图重用模块。
本文的标注规则:
- $(.)^w$ 表示世界坐标系,重力方向与世界坐标系z 轴对齐;
- $(.)^b$ 表示物体坐标系,与IMU 坐标系相同;
- $(.)^c$ 表示相机坐标系;
- 使用旋转矩阵 $\mathbf{R}$ 和四元数 $\mathbf{q}$ 来表示旋转;
- $\mathbf{q}^w_b$ 和 $\mathbf{p}^w_b$ 分别表示从物体坐标系到世界坐标系的旋转和平移;
- $b_k$ 表示第k 张图片时刻的物体坐标系,$c_k$ 表示相机坐标系;
- $\mathbf{g}^w = [0, 0, g]^T$ 是世界坐标系下的重力向量;
- 使用 $\hat{(.)}$ 表示某个参数的噪声观测或估计值。
4 Measurement Preprocessing
观测预处理步骤:
- 对于视觉观测:跟踪连续帧之间的特征,并在最新帧中检测新的特征;
- 对于IMU 观测:对连续帧之间的IMU 进行预积分。
4.1 Vision Processing Front End
对每张新图片,使用KLT 稀疏光流法来跟踪已有的特征;此外,检测新的角点特征来维持图片的最小特征数量(100-300)。探测器通过设定一个特征间最小像素间隔来执行特征均匀提取,2D 特征首先经过去畸变、外点剔除,然后投影至一个单位球上,外点剔除是通过RANSAC 方法实现的。
关键帧选取标准有两个:
- 较前一个关键帧的平均视差:若当前帧与上一个关键帧之间的平均视差超过一定阈值,则将当前帧设为关键帧;值得注意的是,平移与旋转均可以造成视差,但是纯旋转运动无法对特征进行三角化,为解决该问题,作者在计算视差时使用短期的陀螺仪观测来补偿旋转,需要说明的是,旋转补偿只用于关键帧选取,并不用于VINS 的旋转计算。
- 跟踪质量:如果当前帧跟踪到的特征数量低于一个阈值,则将当前帧设为关键帧。
4.2 IMU Preintegration
作者使用之前工作中用的连续时间基于四元数的IMU 预积分推导方法。
4.2.1 IMU Noise and Bias
IMU 的观测信息是在物体坐标系下的,包含重力和平台的运动信息,此外,观测还包含加速度偏差 $\mathbf{b}_a$ 、陀螺仪偏差 $\mathbf{b}_w$ 以及额外噪声,陀螺仪和加速度计的原始观测量 $\hat{\mathcal{w}}, \hat{\mathcal{a}}$ 如下所示:
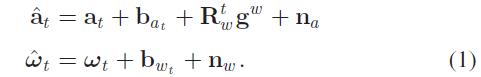
作者假设加速度计和陀螺仪的观测噪声服从高斯分布:$\mathbf{n}_a\sim\mathcal{N}(0, \sigma_a^2), \mathbf{n}_w\sim\mathcal{N}(0, \sigma_w^2)$ ;偏差 $\mathbf{b}_a$ 、 $\mathbf{b}_w$ 被建模为随机游走,其对应导数为高斯白噪声,$\mathbf{n}_{b_a}\sim\mathcal{N}(0, \sigma_{b_a}^2), \mathbf{n}_{b_w}\sim\mathcal{N}(0, \sigma_{b_w}^2)$ 。
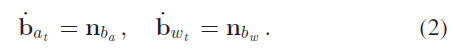
4.2.2 Preintegration
连续两帧图片 $b_k, b_{k+1}$ 之间存在多组惯性观测数据,给定偏差估计,在局部坐标系 $b_k$ 中进行积分:
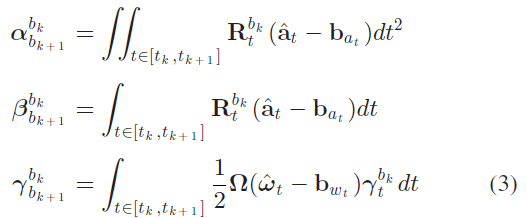
其中:
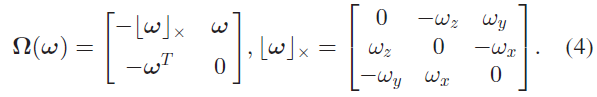
$\alpha, \beta, \gamma$ 的协方差 $\mathbf{P}_{b_{k+1}}^{b_k}$ 也进行相应传递;可以看出预积分项(式3)可通过给定 $b_k$ 作为偏差的参考坐标系,仅用IMU 观测即可获取。
4.2.3 Bias Correction
如果偏差估计改变量较小,利用一阶导数近似进行调整:
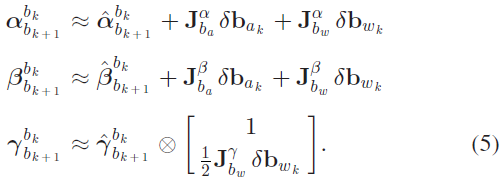
如果偏差估计改变量较大,则在新的偏差估计下进行传递。该策略可为基于优化的算法节省大量计算资源,因为不需要重复进行IMU 观测传递。
5 Estimator Initialization
单目相机紧耦合的VIO 是一个高非线性系统,需要在开始时刻进行准确的初始化估计。作者通过将IMU 预积分和视觉观测进行松对齐来获取必要的初始估计值。
5.1 Vision-Only SfM in Sliding Window
作者控制滑动窗口内的图像帧数来限制计算复杂度,SfM 过程采取以下步骤:
- 首先,确定当前帧与窗口内所有历史帧之间的特征关联,如果可以找到稳定的特征跟踪(超过30个跟踪特征)以及充分的视差(超过20像素),则可利用five-point 算法获取两帧之间的相对旋转和位移;
- 然后,随意设定尺度参数,对两帧中的所有跟踪特征进行三角化,基于三角化特征,使用PnP 算法来估计窗口内其他所有帧的位姿;
- 最终,利用全局BA 来最小化所有观测特征的重投影误差。
由于尚未确定世界坐标系,所以将第一帧图片的位姿 $(.)^{c_0}$ 作为SfM 的参考坐标系,所有图片代表的相机位姿 $(\overline{\mathbf{p}}_{c_k}^{c_0}, \mathbf{q}_{c_k}^{c_0})$ 和特征位置都表示为 $(.)^{c_0}$ 的相对量,给定相机和IMU 之间的外参 $(\mathbf{p}_c^b, \mathbf{q}_c^b)$ ,可将相机位姿从相机坐标系转换至物体坐标系:
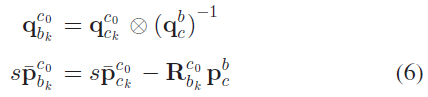
其中,s 是未知的尺度参数。
5.2 Visual-Inertial Alignment
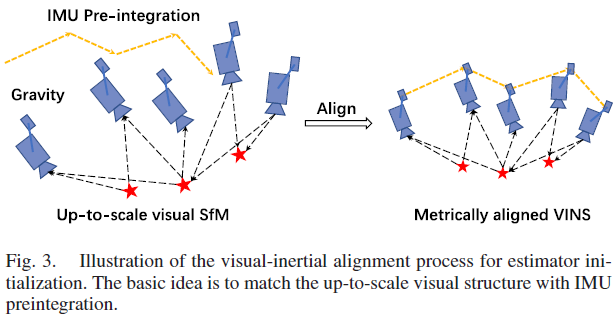
视觉-惯性的对齐过程如Fig. 3所示,基本想法是将视觉SfM 和IMU 预积分匹配起来。
5.2.1 Gyroscope Bias Calibration
假设从SfM 获取窗口内连续两帧 $b_k, b_{k+1}$ 的旋转参数 $\mathbf{q}_{b_k}^{c_0}, \mathbf{q}_{b_k+1}^{c_0}$ ,以及从IMU 预积分中获取两者之间的相对约束 $\hat{\gamma}^{b_k}_{b_{k+1}}$ ,作者将IMU 预积分项做关于陀螺仪偏差的线性化,并最小化下面的损失方程:
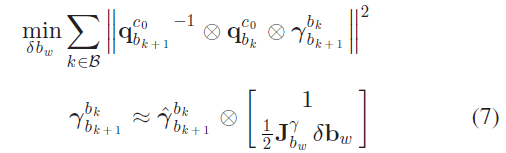
其中,$\mathcal{B}$ 表示窗口内的所有图像帧。这样可以得到陀螺仪偏差 $\mathbf{b}_w$ 的初始标定值,然后使用新的陀螺仪偏差来传递所有的IMU 预积分项 $\hat{\alpha}^{b_k}_{b_{k+1}}, \hat{\beta}^{b_k}_{b_{k+1}}, \hat{\gamma}^{b_k}_{b_{k+1}}$ 。
5.2.2 Velocity, Gravity Vector, and Metric Scale Initialization
在对陀螺仪偏差进行初始化之后,继续对其他导航状态参数进行初始化,包括速度、重力向量以及尺度参数。
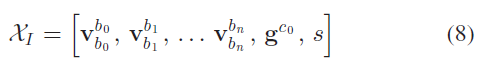
其中,$\mathbf{v}_{b_k}^{b_k}$ 为第k 张图片时在物体坐标系中的速度;$\mathbf{g}^{c_0}$ 表示 $c_0$ 帧的重力向量;s 代表单目SfM 的尺度单位。
对于窗口内的连续两帧 $b_k, b_{k+1}$ ,有以下等式表示:
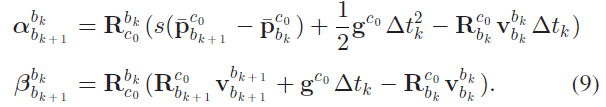
结合式6和式9,得到以下的线性观测模型:
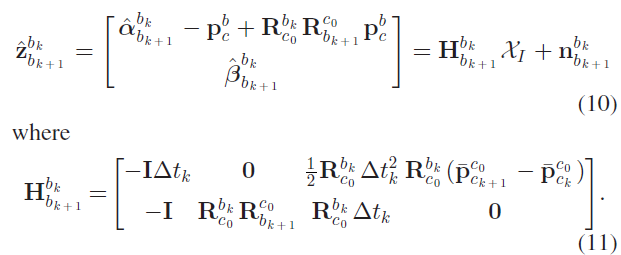
其中,$\mathbf{R}_{b_k}^{c_0}, \mathbf{R}_{b_{k+1}}^{c_0}, \overline{\mathbf{p}}_{c_k}^{c_0}, \overline{\mathbf{p}}_{c_{k+1}}^{c_0}$ 可从单目视觉SfM 获取;$\Delta t_k$ 表示连续两帧的时间间隔。通过求解下面的最小二乘问题可得到每一帧图片代表的物体坐标系下的速度参数、视觉参考坐标系下的重力向量,以及尺度参数:
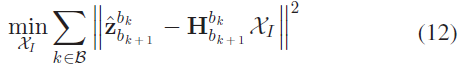
5.2.3 Gravity Refinement
从上述线性初始化中获取的重力向量可通过约束数值大小进行细调,大部分情况下重力向量的大小是已知的,这就导致该重力向量是2自由度的,因此,作者使用正切空间中的两个向量对重力进行扰动:$g(\hat{\overline{\mathbf{g}}} + \delta \mathbf{g}, \delta \mathbf{g} = w_1\mathbf{b}_1 + w_2\mathbf{b}_2)$,其中,g 为重力的已知大小,$\hat{\overline{\mathbf{g}}}$ 表示重力方向的单位向量,$\mathbf{b}_1, \mathbf{b}_2$ 为正切平面上的两个正交偏差,如Fig. 4所示,$w_1, w_2$ 为两个方向上的扰动值。
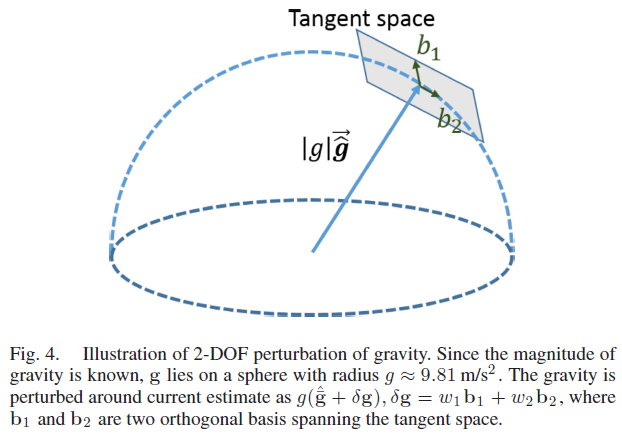
使用 $g(\hat{\overline{\mathbf{g}}} + \delta \mathbf{g})$ 替代式9中的 $\mathbf{g}$ ,与其他参数共同求解2自由度的 $\delta \mathbf{g}$ 。
5.2.4 Completing Initialization
在细调重力向量之后,通过将重力向量对齐世界坐标系的z 轴,来获取世界坐标系和相机坐标系 $c_0$ 之间的旋转参数 $\mathbf{q}_{c_0}^w$ ,然后即可将获取到的所有参数从相机坐标系转换至世界坐标系。至此,系统初始化完成。
6 Tightly Coupled Monocular VIO
基于滑动窗口的紧耦合单目VIO 进行高精度与鲁棒状态估计,过程如Fig. 5所示:
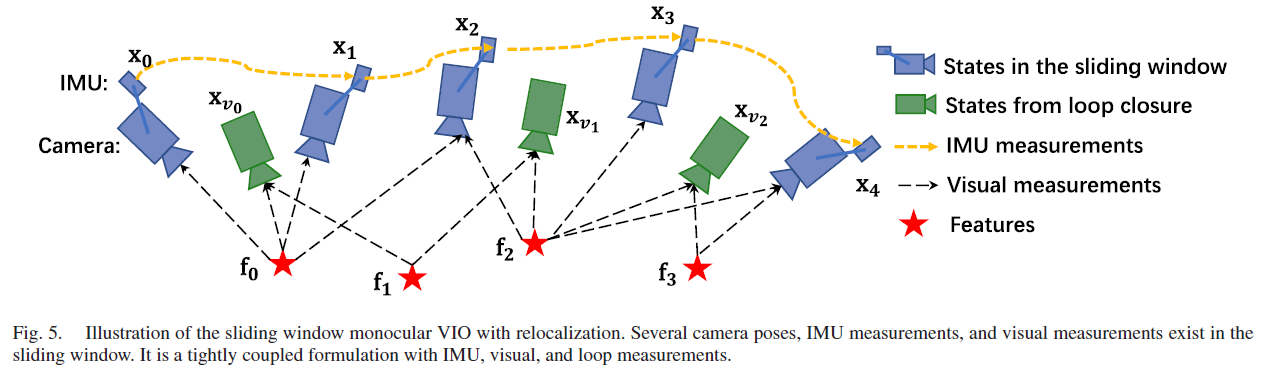
6.1 Formulation
滑动窗口内的状态向量定义为:
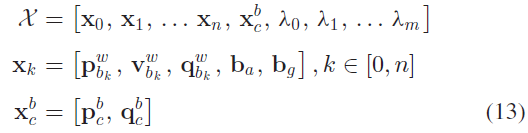
其中,$\mathbf{x}_k$ 表示第k 张图片代表的IMU 状态,包含世界坐标系下的位置、速度及朝向,以及IMU 物体坐标系下的加速度偏差和陀螺仪偏差;n 表示关键帧的总数;m 表示窗口内的特征总数;$\lambda_l$ 表示第 l 个特征在首次观测的逆距离。
作者使用视觉-惯性BA 方程,最小化先验和所有观测残差M 范数的总和来获取最大后验估计:
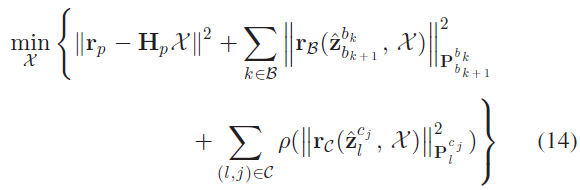
其中,$\mathbf{r}_{\mathcal{B}}, \mathbf{r}_{\mathcal{C}}$ 分别表示IMU 和视觉观测的残差;$\mathcal{B}$ 表示所有的IMU 观测;$\mathcal{C}$ 表示当前滑动窗口内至少被观测2次的特征集合;$\{\mathbf{r}_p, \mathbf{H}_p\}$ 表示边缘化先验信息。本系统使用Ceres 求解非线性问题。
6.2 IMU Measurement Residual
考虑在窗口内连续两帧间 $b_k, b_{k+1}$ 的IMU 观测,其预积分残差可被定义为:
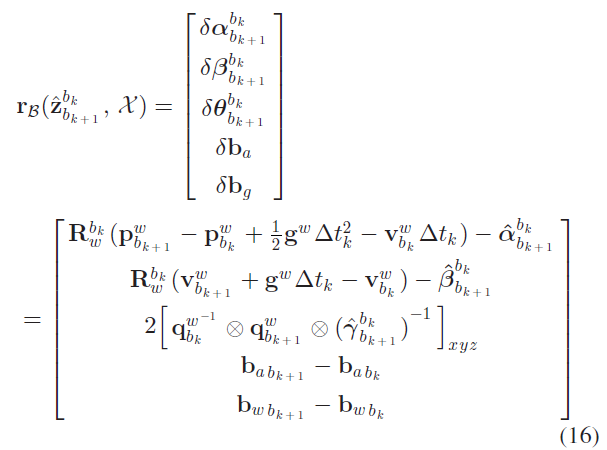
其中,$[.]_{xyz}$ 表示提取误差状态表示四元数的向量部分;$\delta \theta ^{b_k}_{b_{k+1}}$ 表示四元数的3D 误差状态表示; $[\hat{\alpha}^{b_k}_{b_{k+1}}, \hat{\beta}^{b_k}_{b_{k+1}}, \hat{\gamma}^{b_k}_{b_{k+1}}]$ 表示IMU 预积分观测项。
6.3 Visual Measurement Residual
相较于传统针孔相机模型将重投影误差定义在一个图像平面上的做法,本文作者将相机观测残差定义在一个单位球上。几乎所有类型相机的光学特性(包括广角相机、鱼眼相机、全向相机等)都可以建模为连接单位球表面的单位射线。假设第 $l$ 个特征是在第 $i$ 帧图片被首次观测到,则该特征在第 $j$ 帧图片上的观测残差定义为:
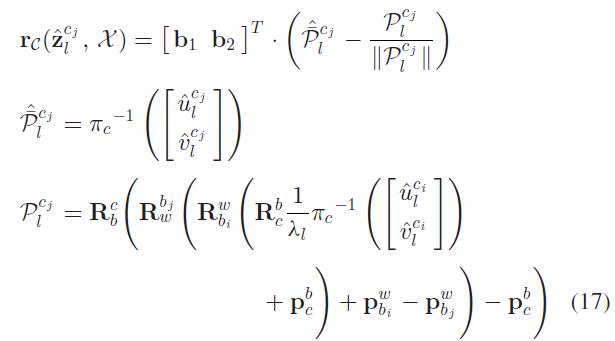
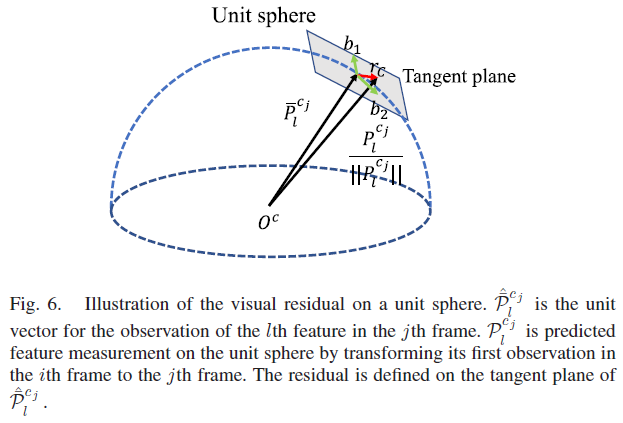
其中,$[\hat{u}^{c_i}_l, \hat{v}^{c_i}_l]$ 表示第 $l$ 个特征在第 $i$ 帧图片被首次观测到的像素坐标;$[\hat{u}^{c_j}_l, \hat{v}^{c_j}_l]$ 表示该特征在图片 $j$ 中的像素坐标;由于视觉残差是2自由度的,所以作者将残差向量投影至正切平面,$\mathbf{b}_1, \mathbf{b}_2$ 表示 $\hat{\overline{\mathcal{P}}}^{c_j}_l$ 正切平面上的两个正交向量,如Fig. 6所示;式14中的协方差 $\mathbf{P}_l^{c_j}$ 也从像素坐标系传递至单位球上。
6.4 Marginalization
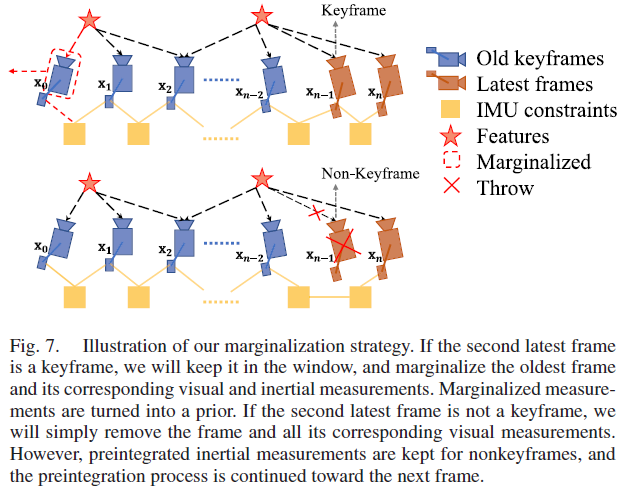
为了限制计算复杂度,作者使用边缘化策略,有选择性地从滑动窗口中边缘化掉IMU 状态 $\mathbf{x}_k$ 和特征 $\lambda_l$ ,同时将对应观测的边缘状态量转换为先验信息。边缘化过程如Fig. 7所示,作者选择不边缘化掉非关键帧的所有观测是为了保持系统的稀疏性;本系统的边缘化策略是为了保持窗口内关键帧的分隔状态,以保证特征三角化所需的充分视差,以及大激励加速度计观测的概率。边缘化是通过Schur complement 实现的。
6.5 Motion-Only Visual-Inertial Optimization for Camera-Rate State Estimation
由于非线性优化对算力的要求,低算力设备(如手机等)上的紧耦合单目VIO 无法实现相机采集率级别的输出,因此,除了full optimization 外,作者还实现了一个轻量级motion-only visual-inertial 优化来提高状态估计的速率至30Hz。
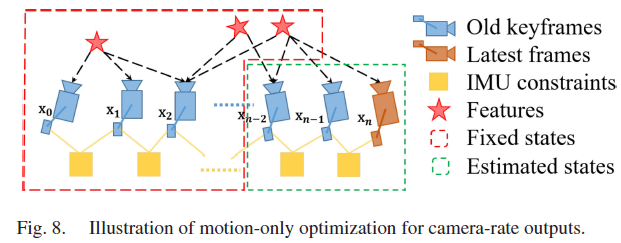
该轻量级优化方法的损失函数与单目VIO 相同(式14),但不会优化窗口内的所有参数,而是只优化几个的最新IMU 状态的位姿与速度;在优化中会使用所有的视觉和惯性观测信息,这会实现较单帧 PnP 方法更为顺滑的状态估计解,该方法的介绍如Fig. 8所示。
两种优化方法的速度对比:在最新的嵌入式电脑中,full optimization 的处理时间约为50ms,而该轻量级优化的处理时间约为5ms。
6.6 IMU Forward Propagation for IMU-Rate State Estimation
本文提出的VIO 输出频率被限制到相机采集速率上,但是仍然可以使用附近的IMU 观测信息来直接传递最新的VIO 估计,以实现IMU 采集速率级别的输出表现。高速率状态估计可被用于回环的状态反馈,作者使用该方法测试了无人机飞行试验。
7 Relocalization
本系统采用了滑动窗口和边缘化策略来限制计算复杂度,但同时也引入了累积漂移;为了消除累积漂移,作者提出了一种可与单目VIO 无缝集成的紧耦合重定位模块。重定位过程首先使用回环检测模块来判断某场景是否出现过,然后建立回环候选帧与当前帧之间的特征级关联,这些特征关联紧耦合至单目VIO 模块,在使用最小计算的情况下实现无漂移状态估计。对多个特征的多次观测可被直接用于重定位,以实现更高的定位精度与顺滑度。重定位过程如Fig. 9 (a)所示。
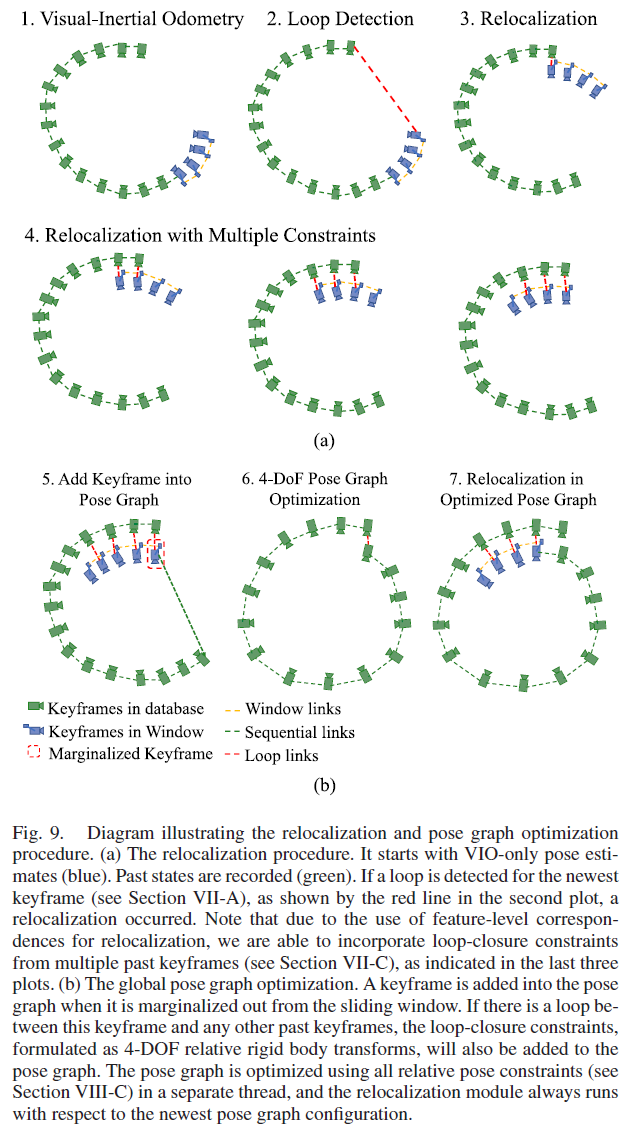
7.1 Loop Detection
作者使用DBoW2 进行回环检测,除了用于单目VIO 的角点特征外,还使用额外500个BRIEF 描述子代表的角点特征,以实现更高的回环检测召回率。经过时间与几何维度的一致性检验后,DBoW2 输出若干个回环检测候选帧。本系统保留所有的BRIEF 描述子以进行特征恢复,但为了节约内存消耗会舍弃所有的原始图像数据。
7.2 Feature Retrieval
当检测到回环后,局部窗口与回环候选帧之间会通过恢复特征关联(BRIEF 描述子匹配)建立联系,作者使用两步的几何外点方法来剔除错误匹配,如Fig. 10所示:

- 2D-2D:利用RANSAC 进行基础矩阵测试;
- 3D-2D:利用RANSAC 进行PnP 测试,基于窗口内特征点的已知3D 位置及回环候选帧中的2D 观测进行PnP 测试。
7.3 Tightly Coupled Relocalization
在重定位中,本系统将所有回环帧的位姿设为常量(不进行优化),使用所有的IMU 观测、局部视觉观测,以及恢复的特征关联对窗口进行联合优化。其中,视觉观测模型与式17相同,除了回环帧的位姿 $(\hat{\mathbf{q}}_v^w, \hat{\mathbf{p}}_v^w)$ 被设为常量,该常量来自位姿图,或直接取自里程计输出(若是第一次重定位)。基于此,将式14更改为如下所示:

其中,$\mathcal{L}$ 表示从回环帧中恢复的特征观测,$(l, v)$ 表示在回环帧 $v$ 中观测到的第 $l$ 个特征。
8 Global Pose Graph Optimization and Map Reuse
在重定位之后,使用额外的位姿图优化来确保历史位姿保持全局一致。
8.1 Four Accumulated Drift Direction
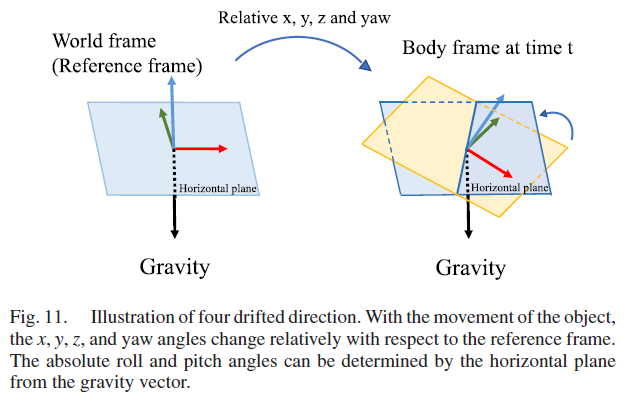
受益于对重力的惯性测量,roll 与 pitch 角度可在VINS 中得到完整观测,如Fig. 11所示,随着物体运动,物体的 3D 位置和旋转会在参考坐标系下发生相对变化,可通过重力向量判断水平面,从而实现对roll 和 pitch 角的确定。因此,累积漂移仅出现在 $x, y, z, yaw$ 上,为了充分利用已知信息来校正漂移,作者固定roll 和 pitch 角度,利用位姿图实现对4自由度的优化。
8.2 Adding Keyframes Into the Pose Graph
关键帧在VIO 处理之后被添加进位姿图中,每个关键帧在位姿图中都作为一个顶点,与其他顶点之间有两种类型的边,如Fig. 12所示。
- Sequential Edge:一个关键帧会与之前的关键帧之间建立序列边,序列边表示两帧之间的相对位姿转换,该转换直接取自于VIO,且该转换关系只包含平移 $\hat{\mathbf{p}}^i_{ij}$ 和yaw 角 $\hat{\psi}_{ij}$;
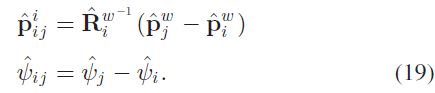
- Loop-Closure Edge:回环边的值来自重定位,同样也只包含平移和yaw 角的4自由度参数。
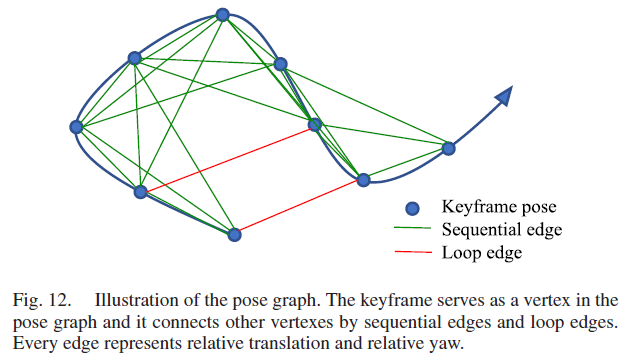
8.3 4-DOF Pose Graph Optimization
定义两帧间边的残差为:
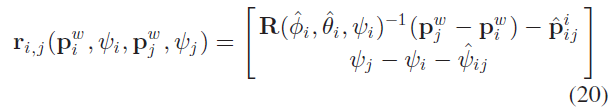
其中,$\hat{\phi}_i, \hat{\theta}_i$ 分别是固定的roll pitch 角。
序列边和回环边的联合损失函数如下式所示:
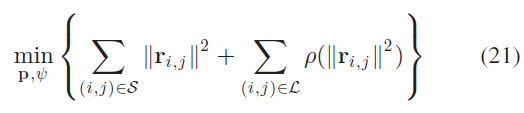
尽管紧耦合的重定位模块已经对回环检测进行了筛选,作者还是增加了Huber 核函数 $\rho(.)$ 来进一步减少错误回环带来的影响。相对应的,序列边部分不使用额外处理,这是因为VIO 已经包含了充足的外点剔除机制。
位姿图优化和重定位在两个独立线程进行异步运行,这使得重定位可以使用最新处理过的位姿图优化结果。
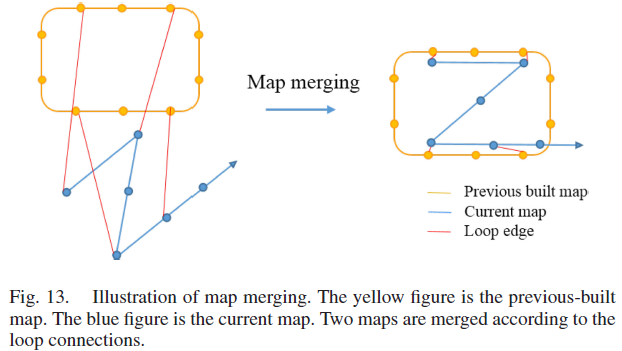
8.4 Pose Graph Merging
位姿图不仅可以优化当前地图,而且还可以利用回环检测将当前地图与历史构建地图进行融合,如Fig. 13所示。