Yang, Shichao, and Sebastian Scherer. “CubeSLAM: Monocular 3-D Object SLAM.” IEEE Transactions on Robotics 35, no. 4 (August 2019): 925–38. https://doi.org/10.1109/TRO.2019.2909168.
1 Introduction
本文作者提出了一个可以同时应用于静态与动态场景中,将2D、3D 物体检测与SLAM 位姿估计相结合的系统,如Fig. 1所示。前提假设:物体立方体经投影后会与2D bbox 相吻合;在此假设下,当给定检测到的2D 物体时,作者利用vanishing point (VP) 产生3D 立方体 proposals,然后通过多视角BA ,利用点和相机对立方体进行进一步的优化。
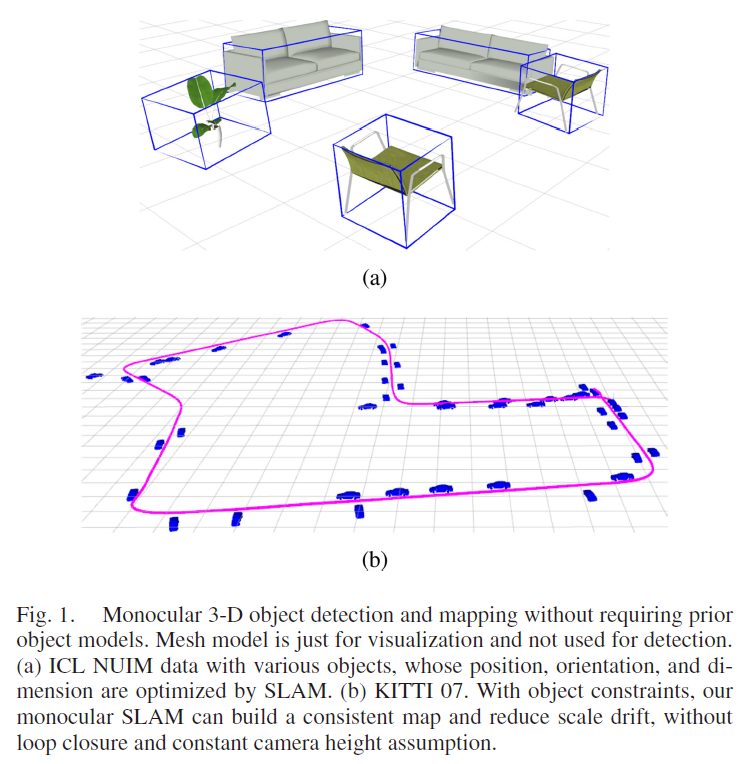
物体在本系统中的作用有两个方面:
- 在BA 过程中提供几何和尺度约束;
- 为难以进行三角测量的点提供深度初始化信息。
在动态场景中,本系统不是简单地将动态观测物体视为外点,而是基于动态点观测与运动模型约束,联合优化相机与物体的轨迹。
本文做出的贡献总结如下:
- 不使用先验物体模型的高效、准确以及鲁棒的单张图片3D 物体检测方法;
- 提出了一种在相机、物体与点之间使用新颖的观测手段的object SLAM 方法,在许多数据集上实现了更好的位姿估计;
- 实验结果证明物体检测与SLAM 两者相互促进;
- 一个在动态场景中利用移动物体来提高位姿估计的方法。
3 Single Image 3-D Object Detection
3.1 3D Box Proposal Generation
3.1.1 3D Box Proposal Generation
一个通用的3D 立方体有9自由度:位置 $\mathbf{t} = [t_x, t_y, t_z]$ ,旋转矩阵 R,以及三维尺度 $\mathbf{d} = [d_x, d_y, d_z]$ 。前提假设:立方体的角在图像上的投影与2D bbox 紧密重合。在该假设下,2D bbox只能提供4个约束(4条边),无法构建9自由度的立方体。已有文献利用预先提供或预测的尺度信息和物体朝向信息作为额外的约束,作者选择使用消失点 VP 来减少回归参数,以适用于通用物体。
消失点 VP 是平行线在透视图像上的交点,3D 立方体有3个正交轴,因此经过投影可形成3个VP,投影过程依赖于相对于相机坐标系的旋转矩阵 R 和相机内参 K:
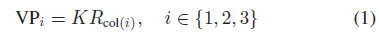
其中,$R_{col(i)}$ 表示R 的第 i 列。
3.1.2 Get 2D Corners From the VP
对于一个立方体,单一视角下最多可同时观测到其3个面,基于观测到的面数量,作者分为三组情况,如Fig. 2所示。
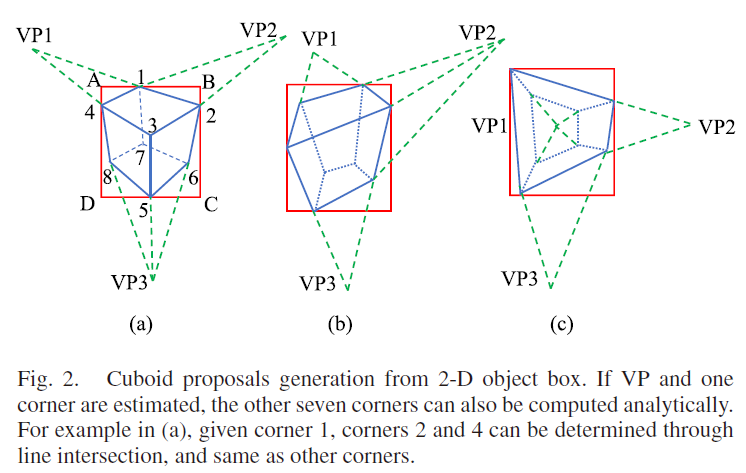
作者以Fig. 2(a)的情况说明,如何基于VP 获取立方体的8个2D 角点:假设VP 和角点 $p_1$ 已知或已被估计,则有 $p_2 = (VP_1, p_1) \times (B, C)$ , $p_4 = (VP_2, p_1) \times (A, D)$ , $p_3 = (VP_1, p_4) \times (VP_2, p_2)$ ,其余2D 角点均可通过类似方法获取,其中 $\times$ 表示两直线的交点。
3.1.3 Get 3D Box Pose From 2D Corners
在获取了2D 角点之后,需要进一步获取立方体的3D 角点,作者分两种情况进行讨论:
情况一 任意位姿的物体:作者使用PnP solver 来求解通用立方体的3D 位置和维度(缺少尺度参数,因为是单目相机)。在物体坐标系(原点设在物体中心)中,3D 立方体的8个顶点坐标可表示为 $[\pm d_x, \pm d_y, \pm d_z]/2$ ,则2D 角点 $p_1$ 可由相应的3D 角点通过下式获取:
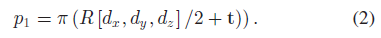
其中,$\pi$ 表示相机投影方程。则式2可提供两个约束(2D 坐标分别代表两个约束方程),那么,选取4个邻接角点(如1,2,4,7)即可得到全约束方程(除了尺度参数)。
情况二 位于地面上的物体:对于位于地面上的物体,可以大幅简化情况一的求解过程并获取尺度参数。在地平面上构建世界坐标系,则物体的roll/pitch 角均为0,这里不再使用复杂的PnP solver,而是直接将8个2D 角点逆投影至3D 地平面,然后计算其他垂直角,从而组成一个3D 立方体;该方法高效且有解析表达式,如位于3D 地平面上的角点5,使用 $[\mathbf{n}, m]$ 来表示(相机坐标系的法向量和距离),则3D 角点 $P_5$ 可通过求逆投影线 $K^{-1}p_5$ 与地平面的交点获取:
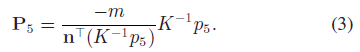
尺度参数由投影过程中相机的高度来决定。
3.1.4 Sample VP and Summary
经过上述分析,3D 立方体的估计问题变为了如何获取三个VPs 以及一个 2D 角点。从式1可得,VPs 通过物体旋转矩阵获取,尽管可通过深度学习来预测物体的旋转矩阵,但是为了更好的泛化性,作者选择手动采样旋转矩阵,并对它们进行评分。本文只考虑位于地面上的物体,因此只需要相机的roll/pitch 角和物体的yaw 角,对于多视角视频数据,作者使用SLAM 来估计相机位姿,因此使得采样空间大幅减小且更为准确。
3.2 Proposal Scoring
在获取了许多立方体proposals 后,作者定义损失函数来进行评分,如Fig. 3所示。

作者提出了不同的损失函数,如语义分割、edge distance、HOG 特征等,最终,作者使用了将立方体和图片边特征进行对齐的快速有效的损失函数,该方法对于具有清晰边缘的物体效果较好,但是由于VP 和鲁棒边滤波的约束,使得其对于自行车、马桶等效果也不差。
将图片记为 $I$ ,立方体表示为 $O = \{R, \mathbf{t}, \mathbf{d}\}$ ,损失函数表示为:
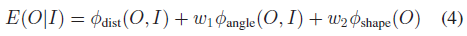
其中,$\phi_{dist},\phi_{angle},\phi_{shape}$ 代表三个损失项,$w_1=0.8, w_2=1.5$ 表示权重参数。
3.2.1 Distance Error $\phi_{dist} = (O, I)$
作者认为,立方体的2D 边应该与实际图片中的边相吻合;首先检测Canny 边,并基于此构建一个distance transform map;然后对立方体的每个可见边(Fig. 2(a)中的蓝色实线边)均匀采样10个点,归纳所有的距离地图值并除以2D bbox 的对角线。
3.2.2 Angle Alignment Error $\phi_{angle}(O, I)$
distance error 容易受到噪声影响,如物体表面的纹理会被识别成边,因此,作者也检测长线段(Fig. 3 中的绿线),并测量它们的角度是否与VP 对齐;首先基于点线关系将这些线与三个VPs 中的一个相关联,对于每个VP,可以找到最外侧的两个线段(分别具有最大、最小的坡度slope),分别记为 $
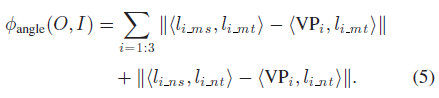
3.2.3 Shape Error $\phi_{shape}(O)$
同一组2D 角点也许会生成相当不同的3D 立方体,因此,作者对具有较大长宽比的立方体增加了一个惩罚项:
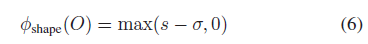
其中,$s = max(d_x/d_y, d_y/d_x)$ 表示物体长宽比;阈值 $\sigma$ 设为1;上式表示若物体长宽比为1,则该惩罚项为0。
4 Object SLAM
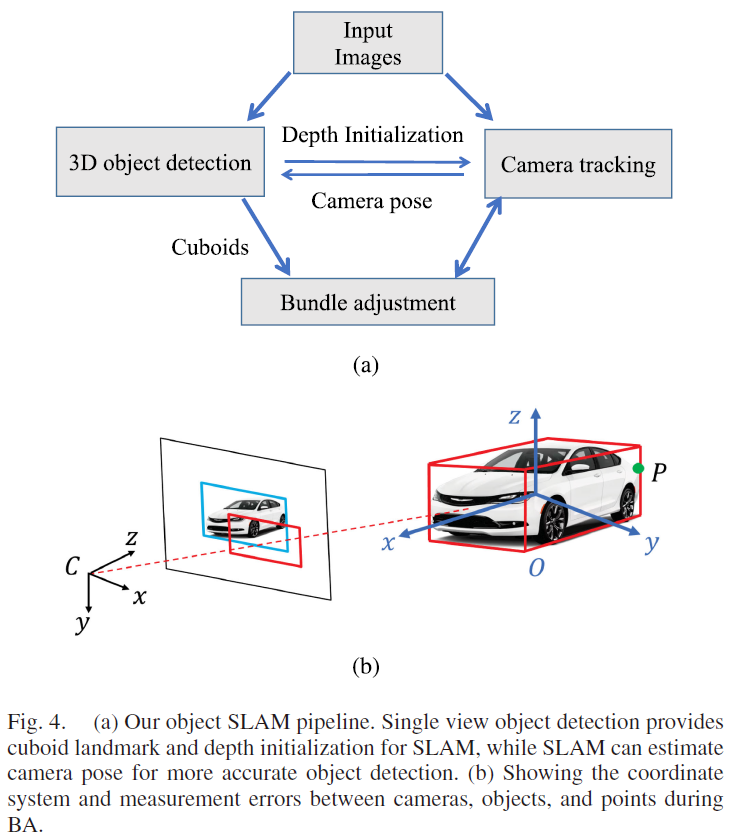
作者将单图片3D 物体检测扩展至object SLAM中对物体和相机位姿进行联合优化,系统基于ORB-SLAM2 搭建的,包括前端相机跟踪和后端BA,作者主要对BA 部分进行修改以包含物体、特征点和相机位姿;值得注意的是,本节内容只使用静态物体。
4.1 BA Formulation
作者提到,除了使用物体进行约束外,还是用了特征点,这是因为仅靠物体难以完整约束相机位姿。相机位姿、3D 立方体和特征点集合分别表示为:$C = \{C_i\}, O = \{O_j\}, P = \{P_k\}$ ,则BA 可表示为以下的非线性最小二乘优化问题:
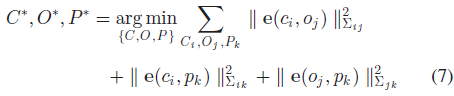
4.2 Measurement Errors
4.2.1 Camera-Object Measurement
作者提供两种观测误差:
3D Measurements
当3D 物体检测较准确时(如使用RGB-D 相机时)使用3D 观测误差。从单张图片检测到的物体位姿 $O_m = (T_{om}, \mathbf{d}_m)$ 作为相机坐标系下的物体观测信息,然后将物体地标转换至相机坐标系以计算观测误差:
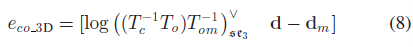
其中,log 将SE3 误差映射至 6 自由度的切向量空间,因此 $e_{co-3D} \in \mathbb{R}^9$ 。
值得注意的是,由于没有先验物体模型,本文使用的基于图片的立方体检测不能区分物体的前后方向,因此,对于式8,需要沿着物体z 轴旋转 $0, \pm90^o, 180^o$ 寻找最小的误差值。
2D Measurements
对于2D 观测,作者将物体地标投影至图片坐标系中以获取2D bbox,如Fig. 4(b)中的红色长方形表示,然后与2D 物体检测bbox (蓝色长方形)进行比较。具体来讲,将3D 立方体的8个角点投影至图像坐标系中,寻找xy 坐标轴的极值点组成一个长方形。
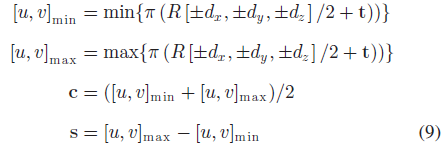
其中,$c, s$ 分别表示2D bbox 的中心坐标和长宽尺寸;因此,4维矩形误差表示为:
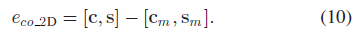
该观测误差较式8表示的3D 观测误差有着小得多的不确定性,因为2D 物体检测相较于3D 检测通常更准确;但同时也丢失了不少信息,因为许多不同的3D 立方体可以投影为相同的2D 矩形,因此需要更多观测信息来约束相机位姿和立方体。
作者表示,由于复杂的检测过程,对误差协方差矩阵 $\sum$ 或者Hessian 矩阵 W 的建模和估计相较于特征点来说要更难,因此,作者对高语义置信度和几何相似物体赋予更高的权重,假设立方体与相机之间距离为 d,物体检测概率为 p,则对于KITTI 数据集设定以下权重参数:$w = p \times max(70-d, 0)/50$ ,其中,70m是截断距离,该参数对不同的数据集会有不同的取值。
4.2.2 Object-Point Measurement
特征点与物体可以相互提供约束,如果点 P 属于某个物体,如Fig. 4(b)所示,则其应该位于3D 立方体内部。作者首先将特征点转换至立方体坐标系中,然后与立方体尺寸进行比较来获取3D 误差:
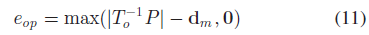
4.2.3 Camera-Point Measurement
使用标准的3D 点重投影误差作为相机-特征点观测误差:
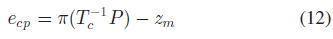
其中,$z_m$ 是3D 点P 的观测像素坐标。
4.3 Data Association
作者提出了一种基于特征点匹配的物体关联,数据关联的步骤如下:
- 首先,如果特征点在至少两帧图片中被观测到位于2D 物体检测框中,且它们距离3D 的立方体中心小于1m 时,将这些特征点与对应的物体关联起来;
- 如果两个物体在不同帧中拥有最多数量的共同特征点,且点的数量超过一定阈值(本文设定为10)时,判定两个物体为同一物体并进行数据关联。
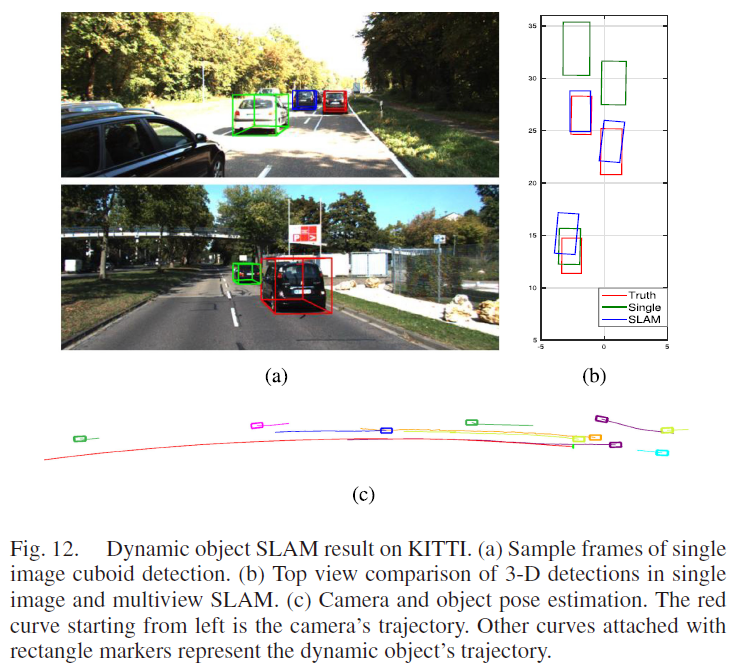
- 需要注意的是,当物体几乎没有与其他帧相关联的特征点时,将该物体判定为动态物体,如Fig. 5中的青色框汽车。

5 Dynamic SLAM
为了减少未知参量让问题可解,作者使用了两个假设:刚体假设与物理运动模型假设。
- 刚体假设是为了保证特征点在关联物体上的位置保持不变,这使得作者可以使用标准的3D 地图点重投影误差来优化位置参数;
- 最简单的运动模型就是匀速运动模型,至于一些特定物体,如自行车,会额外受限于nonholonomic wheel model。
5.1 Notations
作者使用 $^jO^i$ 表示动态物体 $O^i$ 在观测帧 j 中的位姿;对于动态物体 $O^i$ 上的动态特征点 $P^k$ 表示为 $^iP^k$ (物体坐标系),基于刚体假设,其在物体上的位置是固定的。
5.2 SLAM Optimization
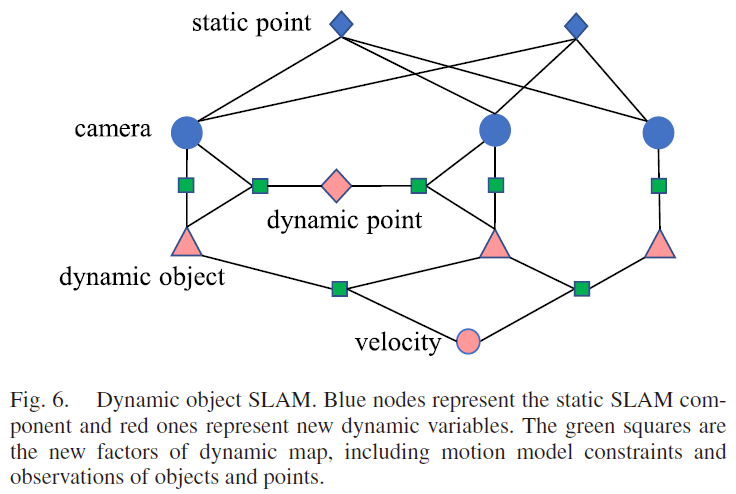
动态物体估计的因子图如Fig. 6所示,其中绿色方框是观测量,包含:camera-object 因子(式10),object-velocity 因子(式14),以及point-camera-object 因子(式15)。
5.2.1 Object Motion Model
3D 物体的通用运动方式可表示为位姿转换矩阵 $T \in SE(3)$ ,作者采用一个更严格的非完整轮模型 nonholonomic wheel model,将汽车运动表示为线速度 $v$ 和转向角 $\phi$ 。假设汽车运动在平面上,则三维向量即可表示完整状态 $T_0 = [R(\theta), [t_x, t_y, o]’]$ ,则根据速度预测的状态表示为:
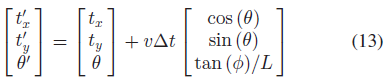
其中,L 表示汽车前后轮中心的距离。最终的运动模型误差表示为:
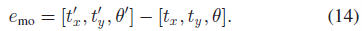
5.2.2 Dynamic Point Observation
对于动态物体上的特征点,首先将其从物体坐标系转换至世界坐标系,再根据相机位姿投影至像素平面,重投影误差表示为:
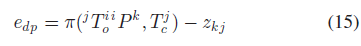
其中,$T^j_c$ 表示相机位姿;$z_{kj}$ 表示观测到的像素坐标。
5.3 Dynamic Data Association
4.3节使用的静态物体数据关联不适用于动态物体,跟踪特征点的经典方法是预测投影位置,然后在附近搜索描述子匹配的特征点,然后检查对极几何约束验证是否匹配正确;但单眼相机动态场景中,很难准确预测物体与特征点的运动,且当物体运动不准确时难以应用对极几何进行计算。因此,作者使用2D KLT 稀疏光流算法进行动态物体特征点的跟踪,该算法并不需要3D 点位置信息。在使用像素追踪之后,考虑物体的运动利用三角测量计算动态特征的3D 位置。
假设两帧图片的投影矩阵为 $M_1, M_2$ ;同一3D 点在两帧对应的位置分别是 $P_1, P_2$ ;对应像素位置分别为 $z_1, z_2$ ;物体在两帧间的运动转换矩阵为 $\Delta T$ 。则有 $P_2 = \Delta T P_1$ ,基于此,有:
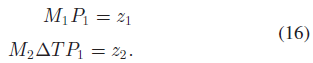
若将 $M_2 \Delta T$ 视为补偿物体运动的相机位姿,则式16可视为标准的两视角三角化问题,可使用SVD 方法进行求解。
值得注意的是,作者提到当像素位移过大时KLT 方法会跟踪失败,因此,对于动态物体跟踪作者直接使用视觉物体跟踪算法:跟踪物体2D bbox,从前一帧预测其在当前帧的大概位置,然后从当前帧的2D bbox 中选取具有最大重叠比例的bbox 实现跟踪。
8 Experiments-Object SLAM
8.1 TUM RGBD and ICL-NUIM Dataset
为了更好地评估单目位姿偏移,作者在使用及结果对比时关掉了ORB SLAM 的回环检测模块。
Fig. 9所示的是在TUM fr3_cabinet 数据集上的实验结果,由于该场景特征点太少,导致现有的单目SLAM 算法均无法完成实验。而本文提出的算法使用object-camera 观测作为额外约束,实现了较好的定位效果。Fig. 9左边下图中估计的立方体存在较大的误差,但经过多视角优化后,3D立方体可以与真实点云实现良好的契合。实验结果如Table 2所示。

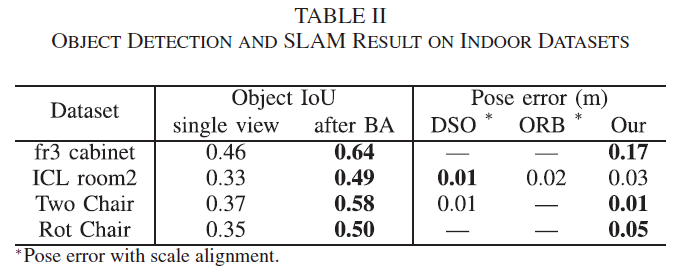
8.2 Collected Chair Dataset

8.4 Dynamic Object